卢晶晶1,陈 曦2,周亚东1,李见春3,李延成3

(1.天津城建大学,天津市建筑结构防护与加固重点实验室,天津 300384; 2.天津大学电气自动化与信息工程学院,天津 300072;3.悉尼科技大学土木工程学院,悉尼 NSW2007)

摘 要:采用自主设计的刚度软化剪切试验测试系统,对各向同性磁流变弹性体(MRE)进行剪 切试验,得到不同电流、频率、位移幅值下的力-位移滞回环;采用 Bouc-Wen模型对 MRE的动态力 学特性进行描述,基于试验数据验证模型的准确性,通过模型分析试验参数对 MRE宏观性能的影 响规律。结果表明:Bouc-Wen模型拟合结果与试验数据吻合较好,剪切力的均方根误差都小于 0.95,说明该模型可以较好地描述 MRE 的刚度软化和阻尼特性。当施加正向电流时,MRE 的刚 度随电流的增大呈线性递减,随频率的增加而增大,当电流大于0.66A 或频率大于1.0Hz时,电 流或频率对刚度的影响程度减弱;MRE 的阻尼随电流的增大而减小,随频率的增大呈指数递减, 当电流大于0.66A 或频率为2.0Hz时,阻尼基本趋于定值。

关键词:磁流变弹性体;刚度软化;Bouc-Wen模型;阻尼 中图分类号:TB381 文献标志码:A 文章编号:1000-3738(2021)01-0100-05

0 引 言

磁流变弹性体(MagnetorheologicalElastomers, MRE)是一种由高分子聚合物和微米级软磁颗粒 制 成 的 磁 流 变 智 能 材 料[1],与 磁 流 变 液 100 卢晶晶,等:基于刚度软化试验建立磁流变弹性体的 Bouc-Wen模型 (MagnetorheologicalFluid,MRF)相比,具有不易沉 降、稳定性好、颗粒耐磨性优良等优点[2],并且其刚 度在外加磁场作用下具有可控性[3]。通过改变通入 线圈的电流大小可以改变磁场强度,进而影响 MRE 的力学性能[4-6],因此 MRE在隔震装置[7]中得到初 步应用,但距离 MRE隔震装置的商业化生产还有一 定的距离。为便于装置的设计和仿真,并推动 MRE 的应用,建立一个合适的磁流变弹性体本构模型来描 述其宏观力学行为是很有必要的。 国内外学者对 MRE在隔震装置上的应用开展 了大量研究。在细观力学模型方面,JOLLY 等[8]首 先提出了磁性颗粒相互作用的磁偶极矩模型,该模型 解释了单链中每一个磁性颗粒的力学行为。CHEN 等[9]对铁磁颗粒的直链模型进行了改进,提出了高斯 分布的有限柱长模型。随后研究者们提出了多种描 述 MRE的细观力学模型,这些模型可很好地解释磁 流变效应机理,但是很难量化 MRE的磁流变效应并 描述其 宏 观 力 学 行 为。在 宏 观 力 学 模 型 方 面,LI 等[10]利用 MRE与钢片制作了一款层叠隔震支座,并 对该支座进行了动态力学性能测试,发现当电流从0 增加到3A 时,该支座的侧向刚度增加了1630%。 为描述这一特性,研究人员将三参数固体模型与改进 的 Maxwell模型相结合,建立了新的机械模型,并对 该支座的滞回特性进行了描述[11-13]。LI等[14]提出了 谐振载荷下 MRE 的四参数力学模型,对各向异性 MRE进行了动态性能测试,发现 MRE在应变幅值 不超过10%、频率小于10Hz时具有线性黏弹性特 性。EEM 等[15] 将 Ramberg-Osgood 模 型 与 Maxwell模型结合,用来表征 MRE 的动力学特性。 基于 MRE 线弹性理论,CHEN 等[16]建立了 MRE 的六参数流变模型,该模型综合考虑了铁磁颗粒与 基质之间的滑 移 效 应,描 述 了 MRE 的 动 力 特 性。 WANG 等[17]建立了五参数黏弹性模型,通过松弛 试验得到模型的各个参数会受到应变的影响,揭示 了 MRE的非线性特性。目前细观力学模型不能直 观描述 MRE的力-位移特性,而直接描述材料力学 行为的宏观力学模型,则主要应用于 MRE 隔震装 置设计、线性与非线性特性研究,用于描述 MRE 刚 度软化特性研究的模型较为少见。 作者基于线圈磁场对永磁铁的反向消磁原理, 自主设计了 MRE 的刚度软化剪切试验系统,并在 不同电流、位移幅值和频率条件下对各向同性 MRE 开展了剪切试验;基 于 Bouc-Wen 模 型 模 拟 MRE 刚度软化过程的本构关系,并验证模型的准确性,通 过模型分析电流、位移幅值和频率对 MRE 宏观性 能的影响规律,为基于 MRE 刚度软化理念的智能 隔震器设计提供理论参考。

1 MRE刚度软化剪切试验

1.1 试样制备与试验方法

试验材料为自主配制的各向同性 MRE,其羰基 铁粉体积分数为 22%,尺寸为 25 mm×25 mm× 5mm,该材料在固化时无磁场,且磁性颗粒随机分 布于聚二甲基硅氧烷(PDMS)基质中。 试验设备为自主设计的 MRE刚度软化剪切试 验测试系统,系统由万能试验机、线圈、永磁铁、力传 感器、位移传感器、数据采集仪6部分组成,具体如 图1所示。万能试验机提供固定幅值、固定频率的 正弦激励信号;2个线圈通过通入电流与永磁铁形 成磁场调控装置;永磁铁为钕磁铁,MRE 固定在永 磁铁两侧,随着永磁铁作剪切运动;力传感器一端通 过连接杆与下夹具连接,测试输出的力信号;位移传 感器获取永磁铁竖直运动位移信号;力传感器与位 移传感器测得的信号通过数据采集仪传输至计算机 中。万能试验机的最大试验力为100kN,线圈电源 型 号 为 兆 信 KXN-1005D,数 据 采 集 仪 型 号 为 WKD3840,位移传感器型号为 YWD-100;力传感器 的精度为1.8994×10 -3。共进行48组试验,测试 系统的正弦激励位移幅值分别为1,2 mm,信号频 率分别为0.1,0.5,1.0,2.0 Hz,提供的电流分别为 -0.45,0,0.20,0.43,0.66,0.90A。 图1 MRE刚度软化剪切试验测试系统 Fig.1 MREstiffnesssofteningsheartestsystem

1.2 试验结果与讨论

由图2可知,MRE 的刚度软化现象较明显,在 相同频率、位移幅值作用下,当线圈上施加正向电流 101 卢晶晶,等:基于刚度软化试验建立磁流变弹性体的 Bouc-Wen模型 时,滞回环的斜率随着电流的增大而减小,当施加反 向电流时,滞回环的斜率随着电流的增大而增大。 力-位移滞回环的斜率表示材料的刚度[8],线圈与永 磁铁形成磁场可调控的装置[18],可通过改变线圈电 流使 MRE发生刚度软化。当线圈上施加正向电流 时,线圈产生的磁场与永磁铁磁场方向相反,随着电 流的增大,线圈产生的磁场逐渐抵消一部分永磁铁 内部的磁场;磁场的减弱导致 MRE 内部铁磁颗粒 排列变得杂乱无章,使得铁磁颗粒之间的相互作用 减小,因此 MRE 刚度减小,力-位移滞回环的斜率 减小。相反,当线圈上施加反向电流时,随着电流的 增大,线圈产生的磁场与永磁铁磁场叠加,磁场增 强,MRE内部铁磁颗粒排列有序,铁磁颗粒之间的 相互作用增强,因此 MRE 刚度增加,力-位移滞回 环的斜率增大。 图2 不同电流下 MRE的力-位移滞回环 频率1 0Hz 位移幅值2mm Fig 2 Force-displacementhysteresisloopsof MRE atdifferent currents frequencyof1 0Hzanddisplacementamplitude of2mm 图3 不同频率下 MRE的力-位移滞回环 位移幅值1mm 电流0 90A Fig 3 Force-displacementhysteresisloopsof MRE atdifferent frequencies displacementamplitudeof1mmandcurrent of0 90A 由图3可以看出,在相同电流和位移幅值作用 下,频率对力-位移滞回环的斜率影响不大,这是因为 频率对 MRE内部铁磁颗粒的排列方式影响不大[19]。 由图4可以看出,在相同电流和频率作用下,位 移幅值为1mm 时 MRE的力-位移滞回环的斜率及 面积小于位移幅值为2mm 时的。MRE 力-位移滞 回环包围的面积表示材料的能量耗散特性,而能量 耗散特性与阻尼有关[8],由此可知,较高位移幅值下 MRE的刚度和阻尼较小。 图4 不同位移幅值下 MRE的力-位移滞回环 电流0 90A 频率0 5Hz Fig 4 Force-displacementhysteresisloopsofMREatdifferent testamplitudes currentof0 90Aandfrequencyof0 5Hz

2 Bouc-Wen模型的建立与参数分析

2.1 Bouc-Wen模型的建立

通过分析 MRE 的力-位移滞回环,可以得出: (1)MRE加载瞬间有瞬时弹性变形,因此模型应包 含弹性元件;(2)力-位移滞回环有滞回现象,因此 模型应包含 Bouc-Wen元件。此外,应变随着时间 的延长而不断增大,因此模型应包含黏性元件[20]。 综上,可采用 Bouc-Wen元件与 Kelvin元件并联模 型来描述 MRE的力学特性,具体模型如图5所示, 模型公式[19]为 F =αk0x+ (1-α)k0z+c0 dx dt (1) dz dt =A dx dt -β dx dt z n-1z-γ dx dt z n (2) 图5 刚度软化 MRE的 Bouc-Wen模型示意 Fig.5 Bouc-Wenmodeldiagramofstiffness-softenedMRE 式中:F 为剪切力;z 为滞变位移;α 为滞回环的线 性程度,一般情况下,α∈(0,1);x 为位移;t 为时 间;αx 为恢复力中弹性力部分;(1-α)z 为纯迟滞 的组成部分;k0 为弹簧的弹性模量;c0 为 MRE 的 黏性系数;A,n,β,γ 均为无量纲参数。A,n,β,γ 主要影响滞回曲线的形状和大小,其中:A 影响最 102 卢晶晶,等:基于刚度软化试验建立磁流变弹性体的 Bouc-Wen模型 大剪切力;n 控制滞回曲线从线性到非线性的过渡, 为满足拟合的要求并减少未知参数的识别,n 取1; β与γ 表征滞回环的形状和大小。

2.2 Bouc-Wen模型的验证

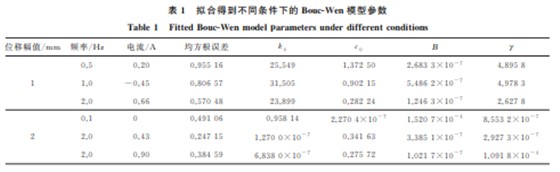
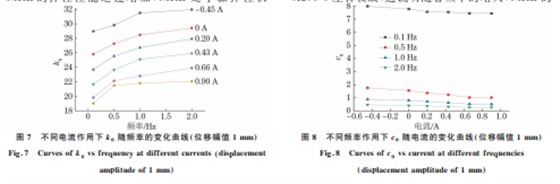
使用 MRE的刚度软化剪切试验数据,采用最小 二乘法,利用 Matlab软件对模型进行参数辨识,拟合 得到不同试验条件下的Bouc-Wen模型参数如表1所 示,部分拟合曲线与试验数据的对比如图6所示。由 表1可以看出,试验数据与模型拟合结果吻合较好, 剪切力的均方根误差都小于0.95,说明拟合效果很 好。该模型可以较好地描述 MRE的力学特性。 图6 不同条件下 MRE刚度软化剪切试验数据与模型 拟合曲线的对比 Fig 6 ComparisonofMREstiffnesssofteningsheartestdata withmodelfittingcurveunderdifferentconditions 表1 拟合得到不同条件下的 Bouc-Wen模型参数 Table1 FittedBouc-Wenmodelparametersunderdifferentconditions 位移幅值/mm 频率/Hz 电流/A 均方根误差 k0 c0 Β γ 0.5 0.20 0.95516 25.549 1.37250 2.6833×10 -7 4.8958 1 1.0 -0.45 0.80657 31.505 0.90215 5.4862×10 -7 4.9783 2.0 0.66 0.57048 23.899 0.28224 1.2463×10 -7 2.6278 0.1 0 0.49106 0.95814 2.2704×10 -7 1.5207×10 -4 8.5532×10 -7 2 2.0 0.43 0.24715 1.2700×10 -7 0.34163 3.3851×10 -7 2.9273×10 -7 2.0 0.90 0.38459 6.8380×10 -7 0.27572 1.0217×10 -7 1.0918×10 -4 2.3 Bouc-Wen模型参数分析 图7 不同电流作用下k0 随频率的变化曲线 位移幅值1mm Fig 7 Curvesofk0vsfrequencyatdifferentcurrents displacement amplitudeof1mm 由图7可知:随着电流的增大,k0 基本呈线性 递减趋势,MRE的刚度软化现象较明显;在频率大 于1.0Hz条件下,当电流大于0.66A 时,k0 随电流 增大而递减的趋势减弱。随着电流的增大,MRE的 弹性性能降低,刚度减小,同时当电流大于0.66A 时,电流对 MRE刚度的影响减弱。随着电流的增大, MRE内部磁场减弱[18],铁磁颗粒之间的相互作用力 减小,MRE整体表现为刚度降低[21] ;而当电流大于 0.66A时,由电流引起的磁场变化对 MRE 刚度的 影响程度降低。k0 随频率的增大呈增大趋势。在 频率 0.1~0.5 Hz时,k0 增 加 速 率 较 大,这 说 明 MRE的弹 性 性 能 迅 速 增 加,MRE 处 于 黏 弹 性 状 态[22] ;当频率大于1 Hz时,k0 随频率增大而增大 的趋势减弱。随着频率的增大 MRE的弹性性能增 大,即 MRE的刚度增大,并且当频率大于1Hz时, 频率对 MRE刚度的影响逐渐减弱,这是因为随着 频率的增大,MRE 内部的铁颗粒链仅在限定的位 置作热振动[22],MRE 出现动态硬化现象[21],因此 MRE整体呈现硬而脆的性能。 图8 不同频率作用下c0 随电流的变化曲线 位移幅值1mm Fig 8 Curvesofc0vscurrentatdifferentfrequencies displacementamplitudeof1mm 由图8可知,c0 随电流的增大呈递减趋势,并 且当电流大于0.66A 时,c0 趋于稳定,这说明随着 电流的增大,MRE 的黏性减弱,即阻尼降低,当电 流大于0.66A 时,阻尼趋于稳定。随频率的增大, c0 呈指数递减趋势,当频率为2.0Hz时,c0 逐渐向 0.2756左右收敛,这说明随着频率的增大,MRE的 103 卢晶晶,等:基于刚度软化试验建立磁流变弹性体的 Bouc-Wen模型 阻尼呈指数递减,并且当频率为2.0Hz时,MRE的 阻尼基本趋于定值。随着频率的增大,铁磁颗粒与 基质之间的摩擦作用加强,MRE 的损耗模量降低, 宏观表现为 MRE的阻尼下降[21]。 Bouc-Wen模型中参数β,γ 表征滞回曲线的形 状和大小[23],随着β+γ、γ-β 的变化,滞回曲线呈 现不同的类型[16]。在试验条件下β+γ>γ-β>0, 滞回曲线类型如图9所示。由图9可知,随位移x 的增大滞变位移z 呈指数递增,且随着频率的增大, 滞回曲线发生顺时针旋转,高度增大。 图9 不同频率作用下z随x 的变化曲线 位移幅值1mm 电流0A Fig 9 Curveofzvsxatdifferentfrequencies displacementamplitudeof1mmandcurrentof0A

3 结 论 (1)Bouc-Wen模型对 MRE 刚度软化特性的 拟合结果与试验数据吻合较好,剪切力的均方根误 差都小于0.95,说明该模型可以较好地描述 MRE 的刚度软化和阻尼特性。 (2)MRE的刚度软化现象较明显,当施加正向 电流时,MRE的刚度随电流的增大呈现递减趋势, 并且 当 电 流 大 于 0.66 A 时,电 流 对 不 同 频 率 下 MRE刚度的影响程度减弱;MRE 的刚度随频率的 增加呈增大趋势,当频率大于1Hz时,频率对不同 电流下 MRE刚度的影响程度减弱。 (3)MRE的阻尼随电流的增大呈现递减趋势, 当电流大于0.66A 时,不同频率下 MRE 的阻尼趋 于稳定;MRE的阻尼随频率的增大呈指数递减,当 频率为2.0Hz时,不同电流下 MRE 的阻尼基本趋 于定值。

来源：材料与测试网