冯擎峰１,姚再起１,叶 拓２,朱 凌１,王震虎２,郭鹏程２,李落星２

(１．宁波吉利汽车研究开发有限公司,宁波 ３１５０００;

２．湖南大学汽车车身先进设计制造国家重点实验室,长沙 ４１００８２)

摘 要:采用分离式霍普金森压杆装置对６０１３ＧT４铝合金在不同温度(２５,２００,３００ ℃)和应变速率(１０００,２０００,３０００,４０００,５０００s－１)下进行了动态压缩试验,研究了该铝合金在冲击载荷作用下的动态力学行为,并采用试验拟合得到的JohnsonＧCook本构方程,对动态冲击试验进行了数值模拟.结果表明:６０１３ＧT４铝合金具有明显的应变速率和应变硬化效应,动态流变应力随变形温度的升高而减小;室温下合金的屈服强度对应变速率不敏感,但随变形温度的升高,屈服强度的应变速率敏感性增强;基于室温准静态与不同温度和应变速率下的动态真应力Ｇ真应

变曲线,确定了铝合金的JohnsonＧCook本构方程;不同温度和应变速率下真应力Ｇ真应变曲线的数值模拟结果与本构方程拟合和试验结果均吻合的较好.

关键词:６０１３ＧT４铝合金;动态力学行为;应变速率敏感性;数值模拟

中图分类号:TG１５６ 文献标志码:A 文章编号:１０００Ｇ３７３８(２０１７)０７Ｇ００８５Ｇ０６

DynamicMechanicalBehaviorandNumericalSimulationof６０１３ＧT４

AluminumAlloyatDifferentTemperaturesandStrainRates

FENGQingfeng

１,YAOZaiqi１,YETuo２,ZHULing

１,WANGZhenhu２,GUOPengcheng

２,LILuoxing

２

(１．NingboGeelyAutomobileResearchDevelopmentCo．Ltd．,Ningbo３１５０００,China;

２．StateKeyLaboratoryofAdvancedDesignandManufactureforVehicleBody,HunanUniversity,Changsha４１００８２,China)

Abstract:Dynamiccompressiontestof６０１３ＧT４aluminumalloywasconductedbysplitHopkinsonpressure

barapparatusatdifferenttemperatures (２５,２００,３００ ℃)andstrainrates (１０００,２０００,３０００,４０００,

５０００s－１),anddynamicmechanicalbehaviorunderimpactloadwasinvestigated．Numericalsimulationofdynamic

impactexperimentwascarriedoutbythefittedJohnsonＧCookconstitutiveequation．Theresultsshowthat６０１３ＧT４

aluminumalloyhadsignificantstrainrateandstrainhardeningeffect,andthedynamicflowstressdecreasedwith

increaseofdeformationtemperature．Theyieldstrengthatroomtemperaturewasinsensitivitytostrainrate．As

deformationtemperatureincreased,thestrainratesensitivityofyieldstrengthgraduallyincreased．Basedonthe

quasiＧstaticatroomtemperatureanddynamictruestressＧtruestraincurvesatdifferenttemperaturesandstrain

rates,JohnsonＧCookconstitutiveequationofthealloywasdetermined．ThesimulatedresultsoftruestressＧtrue

straincurvesatdifferenttemperaturesandstrainrateswereconsistencewiththeexperimentalandconstitutive

results．

Keywords:６０１３ＧT４aluminumalloy;dynamicmechanicalbehavior;strainratesensitivity;numericalsimulation

０ 引 言

与传统钢铁材料相比,铝合金具有密度小、比强度和比刚度高等优点,是实现汽车轻量化的重要材料[１Ｇ３].６０１３铝合金是目前汽车、武器和航空航天领域中应用最为广泛的铝合金之一,该铝合金在服役过程中除了承受室温准静态载荷外,还要面临不同温度下的冲击、爆炸等动态载荷的作用.在动态载荷的作用下,材料的应变速率通常可达到１×１０３ ~

１×１０４s－１.众所周知,材料的力学响应行为随变形温度和应变速率的不同而显著不同[４Ｇ５],而大多数的金属材料都会表现出明显的应变速率效应[６].A３５６、A３５７、F３５７铝合金在动态载荷作用下的流变应力随应变速率的增加而增大,与准静态载荷下的 相 比,其 流 变 应 力 增 加 了 ４％ ~８％[７].LEE

等[１]和 FAN 等[８]在研究６０６１ＧT６铝合金的动态力学响应行为时都发现了该铝合金具有明显的应变速率敏感性,６００５ＧT６铝合金在高应变速率的载荷作用下也表现出类似的特征[９].变形温度在２５~４００ ℃范围内,６０６１ＧT６铝合金的动态流变应力随温度的升高而不断减小[８];变形温度在－１５０~２５ ℃范围内,２０２４ＧT４和７０７５ＧT６铝合金的流变应力随温度的升高而不断减小[１０];武永甫等[１１]采用分离式霍普金森压杆装置研究了７０７５ＧT６铝合金在２５~４００ ℃范围内的流变应力,表明该铝合金的流变应力随变形温度的升高而逐渐减小,但在３５０~４００ ℃时流变应力对温度不敏感.因此,应变速率和变形温度都会影响铝合金的动态力学性能[１２Ｇ１３],且铝合金在不同工况条件下的力学响应规律也并不相同.当应变速率达到１×１０４s－１时,由于局部的温升效应,６０６１铝合金

的流变应力不再增加[１４];文献[１５Ｇ１６]的研究结果表明 LC４和 LY１２ＧCZ铝合金在高应变速率下的流变应力随应变速率的增加而基本不变.

虽然霍普金森压杆装置能够获得材料在高应变速率下的力学行为,但要实现铝合金在汽车、航空航天、武器装备等领域的大规模应用,还需建立有效的力学本构模型来表征其力学响应行为,并能够进行仿真分析.JohnsonＧCook模型简称JＧC模型,其形式简单且考虑了应变速率和温度效应的影响,可以对金属材料的应力响应行为进行比较准确的预测,是现有动

态塑性变形仿真商业软件中最常用的本构模型.目前,国内外对铝合金在动态载荷下的力学行为及本构方程已进行了一定研究[５Ｇ１７],但研究内容比较单一且缺乏系统性,绝大部分研究都是针对室温下的变形行为,很少有关于铝合金在高温冲击载荷下变形行为与仿真分析的报道,特别是工业上应用较广的６０１３铝合金.因此,为了更好地进行结构设计、分析与优化,提高轻量化６０１３铝合金结构在服役过程中的稳定性,作者采用霍普金森压杆装置研究了６０１３ＧT４ 铝合金在不同温度和应变速率下的动态力学行为,同时通过数值仿真技术,探讨了采用JＧC本构模型表征６０１３铝合金在不同温度和应变速率下变形行为的可行性.

１ 试样制备与试验方法

试验材料为商业６０１３铝合金,采用 XJＧ８００卧式金属型材挤压机挤压成截面直径为２５mm 的铝合金棒材,然后进行 T４处理,实测化学成分如表１所示.采用火花放电线切割机在挤压棒材上切割加工出?８mm×４mm 的圆柱形压缩试样,取样位置和显微组织如图１所示,试样的组织呈纤维状分布.

图１ 铝合金试样的取样位置和显微组织

Fig.１ Samplingplace a andmicrostructure b

ofaluminumalloysample

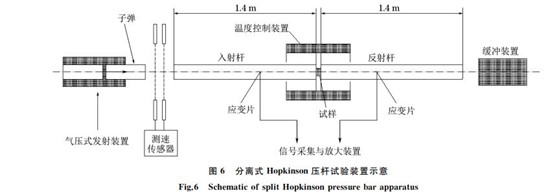
准静态压缩试验在INSTRONＧ４２０６型电液伺服试验机上进行,应变速率为０．００１s－１;不同温度下的动态压缩试验采用分离式霍普金森压杆(splitHopkinsonpressurebar,SHPB)装置,应变速率分别为１０００,２０００,３０００,４０００,５０００s－１,试验温度分别为室温(２５ ℃),２００ ℃和３００ ℃.试验试验数据取３个试样的平均值.试验前在试样表面和压头间涂润滑剂,圆柱形试样放置在入射杆和反射杆之间,通过调节气压室中氮气的气压来控制子弹撞击入射杆的速度,从而实现试验所设定的应变速率.子弹 长 度 为 ２００ mm,入 射 杆 与 反 射 杆 长 度 均 为１４００mm,子弹和压杆直径均为１４mm.

２ 试验结果与讨论

２．１ 力学行为

由图２可知:室温下试验合金的屈服强度对应变速率不敏感,屈服后不同应变速率下的真应力Ｇ真应变曲线呈现一定偏离,表现出一定的应变速率敏感性;准静态载荷作用下,试验合金的流变应力明显低于动态载荷下的流变应力,且屈服后流变应力的增加速率较慢,即合金在准静态载荷下的应变硬化率较低,当真应变增加至０．１７后,流变应力基本不再增加;与准静态载荷作用时相比,动态冲击载荷作用下试验合金的流变应力随真应变的增加而显著增大,且屈服后试验合金动态流变应力的增加速率也明显增大,即在动态冲击载荷作用下试验合金表现出很强的应变硬化效应;在动态冲击载荷作用下,试

验合金的流变应力随应变速率的增加而增大,表现出明显的正应变速率敏感性和应变速率硬化效应;当应变速率增加至５０００s－１时,其流变应力在变形后期不但没有增加,反而略有下降,这可能是由于在该应变速率下动态压缩所引起的局部温升软化大于应变速率硬化和应变硬化的缘故[１８].

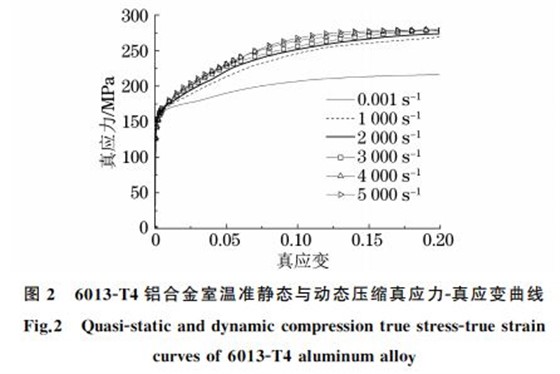
由图３并结合图２可知:试验合金的动态流变应力随变形温度的升高而减小,室温下屈服强度对应变速率不敏感,但随变形温度的升高,屈服强度的应变速率敏感性增强.此外,试验合金在高温下的最大流变应力对应变速率不敏感.

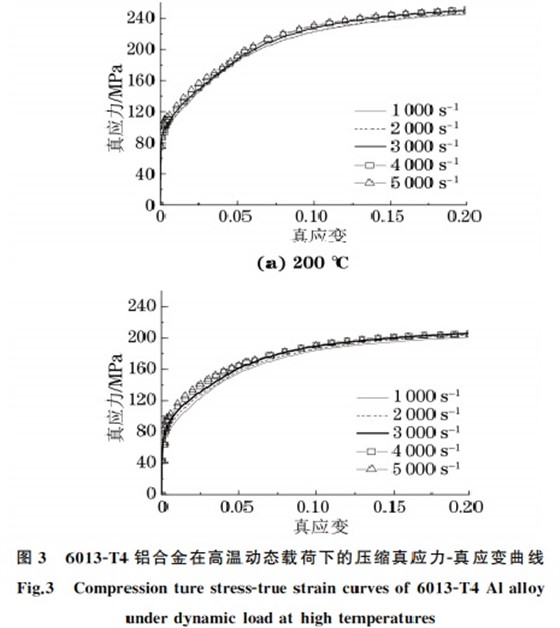
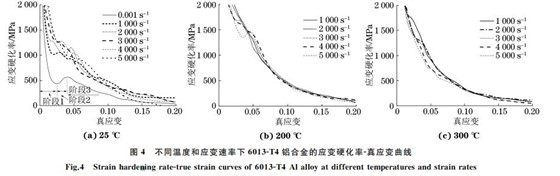
图４为６０１３ＧT４铝合金各温度和应变速率下的应变硬化率Ｇ真应变曲线,表征了合金应变硬化行为的演变过程.由于 SHPB 试验所获得的应力Ｇ应变曲线的弹性段与材料的弹性模量存在偏差,故应变硬化率Ｇ真应变曲线不考虑弹性段[１９].由图可知,在准静态与动态载荷下,试验合金所表现出的应变硬化行为存在显著差异,准静态载荷作用下的应变

硬化率明显低于同温度下动态载荷下的应变硬化率,这表明合金的应变硬化能力具有明显的应变速率效应.准静态载荷下的应变硬化率随真应变的变化趋势可大致分成３个阶段:第１阶段,应变硬化率随真应变的增加而迅速降低;第２阶段,应变硬化率随真应变 的 增 加 而 增 加,一 直 持 续 到 真 应 变 约 为０．０２５;第３阶段,应变硬化率随真应变的增加而缓慢降低.动态冲击载荷下,试验合金在不同温度下的应变硬化行为存在显著差异.室温下试验合金的应变硬化率随真应变的变化关系同样可分成３个阶段,但与准静态载荷下的相比,其应变硬化率的演变规律略有不同,这表现为:第２阶段,随应变速率的增加,应变硬化率基本不变;第３阶段,应变硬化率的下降速度明显加快,这主要是由于在变形中后期,试验合金的应变硬化能力逐渐减弱而绝热温升软化效应不断增加所致.随变形温度的升高,合金屈服后的应变硬化能力逐渐增强,使得原室温下非常明显的第２阶段逐渐消失,当变形温度升高至３００ ℃时,应变硬化率在整个变形过程中均随应变的增加而减小.

２．２ 应变速率敏感性

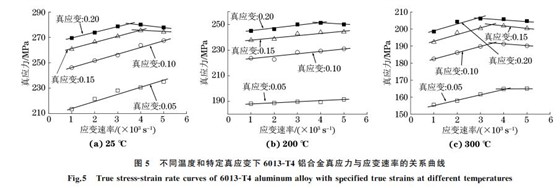
作者选取真应变为０．０５,０．１０,０．１５,０．２０时的真应力与应变速率的关系曲线,研究试验合金的应变速率敏感性.由图５可知:室温和２００℃时,试验合金的真应力与应变速率的关系曲线基本相同,较小应变下的真应力均与应变速率成线性关系,当真应变增加至０．１５和０．２０后,流变应力先随应变速率的增加而增加,当应变速率增加至４０００s－１后,流变应力开始减小.变形温度为３００ ℃时,试验合金４个特定应变下的真应力与应变速率关系曲线的

变化趋势基本相同.流变应力先随应变速率的增加而增大,当应变速率增加至某一临界值后,流变应力开始减小.试验合金流变应力开始减小的临界应变速率随应变的增加逐渐降低.为进一步了解材料的应变速率效应,引入应变速率敏感系数m

[１９].

m ＝(σ２ －σ１)/ln(ε??２/ε??１) (１)

式中:σ２ 和σ１ 分别为相同应变下应变速率分别为

ε??２ 和ε??１ 时的应力.

由表２可知:当变形温度不高于２００℃时,试验铝合金表现出明显的正应变速率敏感性,但在高应变载荷下当变形进行到中后期时,由于绝热温升软化效应,试验合金表现为负的应变速率敏感性.变形温度为３００ ℃时,试验铝合金首先表现为正的应变速率敏感性,在变形进行到中后期时则表现为负的应变速率敏感性.

３ JohnsonＧCook本构模型

JohnsonＧCook模型建立在传统无序金属材料力学性能的基础之上,是针对金属材料在大变形、高

应变速 率 载 荷 下 的 流 变 行 为 提 出 的 一 种 经 验 模型[２０Ｇ２１],其表达式为

σ＝(A ＋Bεn )[１＋Cln(ε??/ε??０)]１－T －TrTm －Tr?è???÷m(２)

式中:A 为材料的屈服强度,B 和n 分别为材料应变硬化模量和硬化指数;C 为材料应变速率强化参数;ε,ε?? 和ε??０ 分别为塑性应变、当前应变速率和准静态参考应变速率;T,Tr 和 Tm 分别为当前温度、参考温度和熔化温度;m 为材料热软化指数.

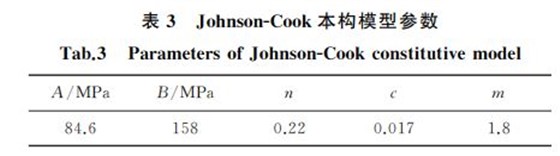
作者选取ε??０＝０．００１s－１为参考应变速率,２５℃为参考 温 度,结 合 不 同 温 度 下 应 变 速 率 分 别 为１０００,３０００,４０００s－１时的真应力Ｇ真应变数据,求得JohnsonＧCook模型的参数,如表３所示.

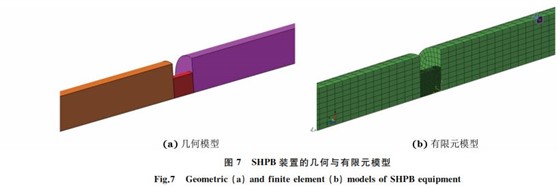
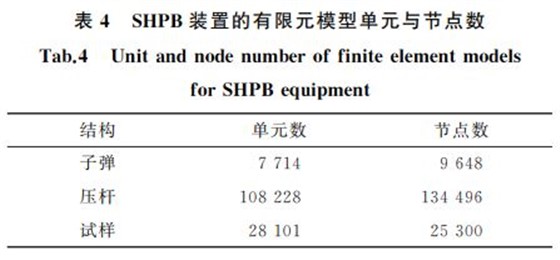
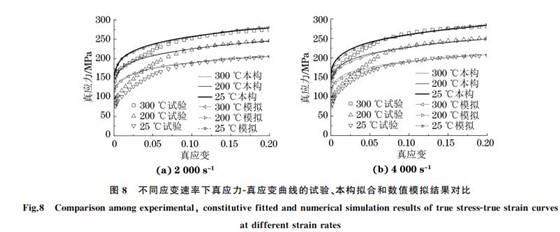
子弹和霍普金森压杆材料为高强钢,采用线弹性材料模型进行模拟,其密度为７．８５×１０－９t??mm－３,弹性模量为２１０GPa,泊松比为０．３.６０１３ＧT４铝合金的动态力学响应行为采用JohnsonＧCook本构模型来描述,其密度为２．７×１０－９t??mm－３,弹性模量为６８GPa,泊松比为０．３３,JohnsonＧCook本构模型参数如表３所示.接触类型选择面面自动接触,忽略各接触面之间的摩擦.为减少沙漏效应,接触算法采用罚函数法.采用将试验所测得的速度直接加载给子弹的方式进行试验的仿真模拟.采集试验数据的应变片位于入射杆与反射杆中间,仿真分析时选取入射杆和反射杆中点的两单元作为输出,得到入射波和反射波的应变Ｇ时间曲线,然后利用两波法重构并得到试验合金的真应力Ｇ真应变曲线.由图８可知:数值模拟、试验及本构模型拟合３种方法得到的试验合金在不同温度和不同应变速率下真应力Ｇ真应变曲线的变化趋势基本相同,试验得到的屈服强度比本构模型拟合和模拟得到的屈服强度明显要低,但在变形中后期,３种方法得到的流变应力偏差较小.以上结果表明,JohnsonＧCook本构模型和有限元模拟可以较准确地得到６０１３ＧT４铝合金在不同温度与应变速率下的动态力学行为.

５ 结 论

(１)与准静态载荷相比,６０１３ＧT４ 铝合金在动态冲击载荷作用下表现出明显的应变速率和应变硬化效应;合金动态流变应力随变形温度的升高而减小;室温下合金的屈服强度对应变速率不敏感,但随变形温度的升高,屈服强度的应变速率敏感性增强.

(２)基于室温准静态与不同温度和应变速率下的动态真应力Ｇ真应变曲线,确定了能够表征６０１３ＧT４铝合 金 在 不 同 应 变 速 率 和 温 度 下 JohnsonＧCook本构方程.

(３)建立了 SHPB 试验的有限元模型,不同温度与应变速率下真应力Ｇ真应变曲线的数值模拟结果与本构方程拟合和试验结果吻合得较好.

材料与测试网-机械工程材料