摘 要:从位错滑移着手并结合晶体结构的特征,从细观层面和宏观唯象层面详细探讨了拉伸变形的本质行为,即微塑性变形具有不同时性和不均匀性,并贯穿于拉伸应力G应变曲线的各个阶段;着重分析了应变速率对拉伸性能的影响,并从刚度修正、应变速率控制等方面探讨了 GB/T228.1-2010的科学性和其在实际运用方面存在的难点及对应的建议.结果表明:拉伸试验各阶段的塑性变形在不同程度上受到应变速率的影响.
关键词:拉伸变形本质;位错滑移;微塑性变形;刚度修正;应变速率
中图分类号:TG115.5+2 文献标志码:A 文章编号:1001G4012(2018)04G0239G05
AnalysisonTestMethodsBaseduponIntrinsicBehaviorofTensileDeformation
LIHuawei,WANGChengzhong
(ShanghaiXiuyangMaterialTestingTechnologyCo.,Ltd.,Shanghai201818,China)
Abstract:TheintrinsicbehavioroftensiledeformationwasdiscussedonmesoGlevelandmacroGlevel,starting
fromdislocationslipandcombining withthecharacteristicsofcrystalstructure.Itisthat microscopicplastic
deformationappearsatdifferenttimesanddistributesindifferentareas,andoccursinallstagesofthetensilestressG
straincurve.Theinfluenceofstrainrateontensilepropertieswasanalyzedemphatically,andthescientificalness,
difficultiesandsuggestionsinpracticaloperationofGB/T228.1-2010werealsoinvestigatedfromtheaspectsof
rigidnesscorrectionandstrainratecontrol.Theresultsindicatethattheplasticdeformationinallstagesoftensile
testwasaffectedbythestrainrateindifferentdegrees.
Keywords:nature oftensile deformation;dislocation slip; microscopic plastic deformation;rigidness
correction;strainrate
金属材料拉伸试验是测试其力学性能的基本方法之一,广泛应用于航空航天、核电、军工、汽车、机械设备、电子器材、医疗器械、建筑等各个行业.自GB/T228.1-2010«金属材料 拉伸试验 第1部分:室温试验方法»实施以来,业界对标准中的部分内容存在着各种各样的争议和解读,仅«理化检验G物理分册»公开发表持各种观点的专题报道就达几十篇之多[1].争议的内容涉及了诸如应力控制、应变控制、弹性阶段的速率、屈服阶段的速率、闭环控制试验机、刚度修正、引伸计、平行长度估算速率等诸多方面[2],这些争议的焦点全都指向了拉伸过程中的速率问题.然而,目前公开发表的文献大多是从宏观唯象层次概括试验事实并得出规律或研究结论,很少有去探究拉伸试验的内在本质,而细观尺度(晶粒、晶界、位错、滑移)是联系宏观尺度(毫米到千米尺度)和微观尺度(原子、电子等基本粒子尺度)的桥梁.为此,笔者尝试从细观尺度的晶粒、晶面、位错、滑移等方面探讨了拉伸试验变形的本质,并结合宏观的试验现象探讨了拉伸试验方法标准中的争议内容.
1 弹性的不完整性完整的弹性应该是加载时立即变形,卸载时立即恢复原状,应力G应变曲线上加载线与卸载线完全重合,即应力和应变同相.但是实际上,弹性变形时加载线与卸载线并不重合,应变落后于应力,存在着弹性后效、滞弹性和包申格(Bauschinger)效应,这些效应的存在说明宏观弹性变形并非理想的弹性变形,即宏观的弹性变形中存在着非弹性变形[3].文献[4]发现了超高强度钢中的晶格微屈服现象,其 研 究 结 果 表 明:规 定 塑 性 延 伸 强 度 Rp0.2 为1160MPa的 某 超 高 强 度 系 泊 链 钢,以 5.5×10-5s-1的应变速率对其进行拉伸试验,拉伸过程中的原位中子衍射测试结果显示其宏观线弹性阶段在应力为700MPa时,(200)晶面族优先于其他晶面出现了非弹性变形,即发生了微屈服[4].文献[5]研究了氢对微屈服的影响,对充氢0.0008%(质量分数)的同类型超高强度系泊链钢(充氢前其同批试样
的Rp0.2为1160MPa),以5.5×10-5s-1的应变速率进行拉伸试验,拉伸至500 MPa时发生脆性断裂,
即该材料只呈现出了宏观线弹性特征.拉伸过程中的原位中子衍射测试结果显示其宏观线弹性阶段在应力为300MPa时,具有(110)取向且平行于拉伸方向(TensileDirection,TD)的晶粒,即(110)//TD取向的晶粒优先于其他取向的晶粒率先呈现了非弹性变形,即出现微屈服现象[5].该现象与文献[6]中的表述相一致,即在外力作用下,部分位错会先达到
临界切应力而滑移(产生微屈服),值得注意的是位错滑移不仅取决于促使位错开动的临界切应力,同时也取决于位错的取向因子μ[6].文献[7]关于位错滑移与弹性变形的表述则更为详细,具有密排六方结构(hcp)的αGTi拉伸试样(纳米长度的单晶试样)的弹性应变为2.68%,原位拉伸过程中随着应变的增加αGTi先后产生了3 种不同 Burgers矢量的滑 移 位 错,其 中 最 先 启 动 的 Burgers 矢 量 为1/3[1210]的位错,其在拉伸应变量很小时(应变为0.44%)即开始滑移[7].非弹性变形、微屈服现象、位错滑移均为塑性变形的表现形式,宏观线性阶段的微屈服现象研究最多的材料当属铍材,有研究者归纳出了铍材产生一个单位(10-6)微屈服σmys与规定塑性延伸强度Rp0.2的经验公式为:Rp0.2=171.0+2.728σmys[8].事实证明拉伸试验的弹性阶段确实存在着塑性变形,弹性性能宏观上呈近似线性特征.
2 弹性的本质
弹性在微观上表现为原子间的作用力与原子间的位移,对于理想晶体而言,由公式 P=Ar2 +Br4 (式中:P 表示原子间的作用力;r 表示原子间距;A 表示原子间吸引力常数,B 表示原子间排斥力常数,A和B 均与原子本性和晶格类型有关)可知,原子间.
3 拉伸试验过程中各阶段变形行为的本质
众所周知,根据非连续屈服试样的拉伸应力G应变曲线特征,为简单起见可将其大致分为4个阶段,即:弹性阶段、屈服阶段、均匀塑性变形阶段、颈缩阶段.当然,对于连续屈服试样,其屈服阶段和均匀塑性变形阶段可认为是一个阶段.由上述弹性的不完整性和弹性的本质分析可知,拉伸试验的宏观弹性阶段也存在微区塑性变形,并贯穿于拉伸试验的各个阶段.塑性变形的主要机制为滑移和孪生,而孪生能够提供的塑性变形量相比滑移来说是非常有限的,在探讨塑性变形时该文主要考虑滑移的影响.
为此,有必要引入以下两个公式[3]
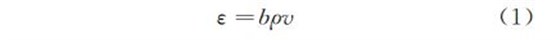
式中:ε 表示塑性应变速率;b 表示位错 Burgers矢量的模;ρ表示位错密度;v 表示位错运动速率.式中:τ为作用于位错滑移面上的切应力;τ0 为位错以单位速率运动所需要的切应力;m 表示位错运动速率的应力敏感性指数.
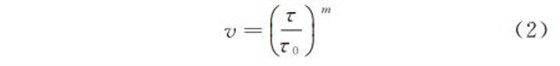
3.1 颈缩阶段
为了叙述的方便同时也考虑到塑性变形的明显性,先分析颈缩阶段的本质.为分析方便,引入一个公式如下
式中:dP 表示拉伸过程中瞬时力值的增加量;A 表
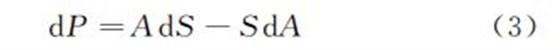
示拉伸试样某时刻的截面积;dA 表示截面积瞬时减小量;S 表示某时刻截面上的应力;dS 表示加工硬化造成的应力瞬时增加量.颈缩前试样平行部分各处的塑性变形宏观上呈近似均匀变形,颈缩开始后变形主要集中于颈部区域,这时dP=AdS-SdA=0,即AdS=SdA,加工硬化和试样截面积的减少对试样承载力的影响达到平衡,力值不再增加,对应拉伸曲线的抗拉强度点位置.随着应变的增加,dP =AdS -SdA < 0,即AdS <SdA,此时试样截面积减小的影响占主导,力值持续减小直至断裂[3].
3.2 屈服阶段和均匀塑性变形阶段
由式(1)可 知,试 样 微 区 的 塑 性 应 变 速 率 由Burgers矢量、位错密度、位错运动速率三者的乘积决定.随着塑性变形的增加,位错密度快速增加使得位错运动速率降低.由式(2)可知,位错运动速率的降低必然会使切应力降低,从而造成试样整体应力的下降[3],这即为拉伸曲线上观察到的上屈服点和屈服下降的本质.屈服的整个过程与上屈服点和屈服下降的本质是一样的,所不同的仅仅是应力的增加与否或增加快慢的问题,而这主要取决于式(3)中的各个变量.式(3)亦可解释连续屈服和非连续屈服,连续屈服时AdS 永远大于SdA,非连续屈服时将多次或者长时间出现AdS=SdA 的现象,从真应力G真应变曲线来看,连续屈服和非连续屈服的图形均为向上的抛物线,两者并无本质区别,反映在人为的日常所见的应力G应变曲线上才出现了连续屈服和非连续屈服现象.值得注意的是,鉴于位错滑移的本质和特性,屈服阶段和均匀塑性变形阶段从细观的层面来研究的话也具有不同时性和不均匀性.为了表述清晰,定义一个微颈缩的概念,即不同时性和不均匀性的位错滑移必将在试样局部微区域产生不均匀塑性变形(局部微区域产生微颈缩).在定义了这样一个概念之后,就可以从细观层面描述屈服阶段和均匀塑性变形阶段,即该阶段自始至终都在不同的微区、不同的时间不间断地产生一个个不同的微颈缩,当某些微颈缩达到一定程度时就不再继续,而未达到微颈缩停止条件的则继续进行,这样一个动态不均匀过程产生了屈服阶段和均匀塑性变形阶段宏观上近似的均匀变形.
3.3 拉伸总体过程的细观与宏观
至此,结合细观和宏观现象,可以对拉伸过程进行总体描述,即整个拉伸过程中均伴随有微区域不同时性和不均匀性的微塑性变形和微颈缩现象,这种微塑性形变和微颈缩的不均匀程度不仅与材料特性相关,同时也与拉伸各个阶段的应变速率或应力速率有关.例如,由于面心立方(fcc)金属具有更多的滑移系,因而在宏观上比体心立方(bcc)金属呈现出更强的均匀塑性变形能力;同时拉伸速率的不同也会影响屈服强度或规定塑性延伸强度.所不同的是各个阶段微塑性变形和微颈缩程度的大小各有不同:弹性阶段由于位错滑移系和滑移量较少,微塑性变形和微颈缩程度较小,反应在宏观层面上即呈近似线性特征,由于该阶段的塑性变形较小,在宏观上的非线性不一定能够被宏观拉伸试验检测出;屈服阶段和均匀塑性变形阶段相比于弹性阶段则呈现出剧烈的微塑性变形和微颈缩,这种微塑性变形和微颈缩分布的不均匀性有时可在宏观上表现出来(如
非连续屈服材料拉伸屈服阶段在使用装卡式引伸计时可能造成的拉伸试验机失控现象[10]);颈缩阶段这种微塑性变形和微颈缩不均匀性表现得最为强烈,直接反映在宏观上的局部颈缩直至断裂(平行长度的某一部分的中心或近中心位置首先形成微孔,并逐渐聚集长大形成微裂纹直至断裂).
4 拉伸速率对拉伸试验的影响
材料屈服强度受拉伸温度和应变速率的影响已有共识,但是在宏观线性阶段拉伸速率对应力G应变曲线的影响尚存在争议[11],鉴于上述分析中微屈服现象贯穿于拉伸过程的各个阶段,而塑性变形的速率对屈服强度有影响,因此可以从理论上推出实际的金属材料不存在理想状态下的绝对线弹性,弹性段的应变速率或多或少也会影响材料的屈服强度.用剪切强度表达的屈服强度公式为[9]
τ=αGbρ (4)
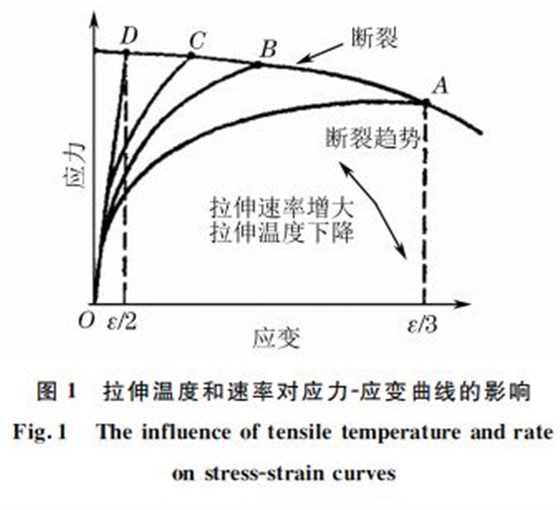
式中:τ为剪切强度;α 为几何常数;G 为剪切模量;b 为位错 Burgers矢量的模;ρ为位错密度.由式(4)可知,材料的屈服强度正比于位错密度和位错 Burgers矢量的模,弹性段也有位错的滑移,也会产生位错的增值或位错密度的增加,因此从这个角度来讲拉伸试验过程中的各个阶段并无本质区别,弹性段的拉伸速率也会影响屈服强度,由于材料对速率的敏感程度不同,这种影响不一定能够被宏观拉伸试验检测出.对于一种确定的材料,拉伸试验应力G应变曲线受温度和拉伸速率的影响,限于篇幅,文献[11]并未把温度和速率的影响单独分开来研究,由图1[12]可知,宏观弹性阶段的拉伸温度和速率不仅影响屈服强度,也影响抗拉强度,甚至还影响材料断裂的性质.
5 GB/T228.1-2010中附录F和刚度修正
刚度修正的问题在业界引起的争议较大,值得注意的是刚度修正首先要忽略拉伸试样的滑动,基于这个前提刚度修正才能成立.