孙明成1,2,张超群1,韩德斌1,2,李宏强1
(1.国网辽宁省电力有限公司电力科学研究院,沈阳 110006;
2.辽宁东科电力有限公司,沈阳 110179)
摘 要:利用 Matlab的优化函数改进了表征应力应变法的优化条件,并优化了表征应力应变法的计算流程,同时利用改进的弹塑性方程对屈服强度σy、应变硬化指数n 和弹性模量E 三个参数同时进行优化,从而确定了材料的力学性能参数,之后采用球形压痕表征应力应变法对 P91钢的力学性能进行测试,并与单轴拉伸试验结果进行对比.结果表明:与单轴拉伸的试验结果相比,采用球形压痕表征应力应变法测得 P91钢力学性能的精度较高,最大偏差值为12.11%.
关键词:球形压痕;表征应力应变法;力学性能
中图分类号:TH140.7 文献标志码:A 文章编号:1000G3738(2017)09G0106G05
0 引 言
通常,材料的力学性能需要用标准试样进行测试后获得,并对试样的尺寸和数量有一定的要求.然而,在对成品设备进行材料力学性能测试时,一般不能进行破坏取样,因此传统的材料力学性能测试技术和手段已经无法满足测试的需要[1G2].
仪器化压痕测试技术(简称压痕法)是在传统的布氏硬度和维氏硬度试验基础上发展起来的新的材料力学性能测试技术.压痕法通过测试和记录压头压入试样过程中的载荷G深度曲线,提供比传统硬度试验更丰富的信息,从而可以获得材料其它的基本力学性能,如弹性模量、屈服强度和抗拉强度等,该技术被誉为“材料力学性能探针”[3].压痕法的优点包括:设备小巧便携,能直接在现场进行力学性能测试;不需要进行破坏取样,能对在役设备进行测试;测试部位微小,可以用于材料局部特性的测定,例如测定焊缝不同区域的力学性能;通过载荷G深度曲线确定材料力学性能,不需要利用光学显微镜测量压
痕.目前,压痕法已应用于许多工程场合中,例如对石油管道、核反应堆压力容器、电站设备等的安全评定[4].
TABOR 在1951年首先提出了材料的力学性能与硬度的关系[5].由于载荷是广度量,应力是强度量,为了测定材料的学性能,压痕载荷必须和相应的接触面积结合起来.在压痕法中,压痕直径不是通过光学显微镜直接测量得到的,而是通过载荷G深度曲线的卸载曲线计算得到的[6].由于球形压头周围存在复杂的三向应力状态,通过理论分析此状态显得十分困难,而且压痕的弹塑性接触问题目前并没有解析解[7G9].因此,作者利用 Matlab的优化函数改进了表征应力应变法的优化条件,优化了表征应力应变法的计算流程,并利用改进的弹塑性方程对屈服强度σy、应变硬化指数n 和弹性模量E 三
个参数同时进行优化,从而确定材料的力学性能参数;采用球形压痕表征应力应变法对 P91钢的力学性能进行 了 测 试,并 与 单 轴 拉 伸 试 验 结 果 进 行 了对比.
1 表征应力应变法
1.1 弹性模量
根据SNEDDON 早期对弹性接触的系统研究,采用压痕法进行测试时,金属材料的弹性模量与弹性接触刚度之间存在如下的关系式塑性变形.弹性变形深度可以通过 OliverGPharr方法计算得到[6].
式中:hd 为弹性变形深度;ω 为压头形状系数,对于平面压头ω=1,锥形压头ω=0.72,抛物线形压头ω=0.75;h∗c 为未考虑材料隆起/凹陷时的深度;a∗为没有考虑隆起/凹陷时的接触半径;R 为球形压头半径.
图2为球形压头压入金属材料表面后的形状示意,图中γ 为压头与试样之间的接触角,a 为考虑隆起/凹陷时的接触半径,hc 为考虑材料隆起/凹陷时的接触深度.压痕处的塑性变形表现为压痕周围的隆起或者凹陷,隆起或者凹陷的程度取决于应变硬化指数n.计算接触半径时需要考虑压头附近材料的隆起或者凹陷所带来的影响,并提出了考虑材料隆起或者凹陷的各种修正方法.无量纲参数c 被HILL引入来考虑材料隆起或凹陷的影响[11].
TABOR提出在完全塑性变形的情况下,压痕的表征应力σr 采用由载荷和接触面积表示的平均应力来代替[5],计算公式为
式中:Ψ 为塑性约束因子,与塑性区的扩展程度,即与材料屈服应变及应变硬化指数有关.在压痕试验中,应力沿三维方向分布,这与单轴拉伸试验不同.通过大量的工作已确定了塑性约束因子 Ψ,在 NPRGISO/TR29381中建议 Ψ=3.
1.4 表征应变
根据压头与材料的接触角来表示表征应变εr.最早的表征应变是由 TABOR 根据经验得出的,如式(10)所示.
式中:K=0.2.TABOR 的表征应变表达式能获得的最大应变值为0.2.AHN 和 KWON 提出了接触边缘剪切应变的概念[4],扩大了表征应变的范围,表征应变被定义为
式中:tanγ 为接触边缘的剪切应变;α 为与材料无关的常数.AHN 和 KWON 建议α=0.1[4],在 NPRGISO/TR29381中则建议α=0.14.经比较,接触边缘剪切应变的表达式是与试验符合较好的一种表达式.因此,作者采用荷兰的压痕法指南中推荐的表征应变表达式,即式(11).
2 计算方法和流程
2.1 分析思路
如果能利用表征应力应变法将球形压痕试验得到的多循环载荷G深度曲线转变成真应力G真应变曲线,就可以确定金属材料的屈服强度、应变硬化指数、弹性模量和抗拉强度等,具体分析思路为:首先采用金属材料弹塑性模型来描述材料的真应力G真应变曲线,不同的材料参数组合对应一系列不同的应力G应变曲线,将这些曲线作为计算曲线;然后将压痕
试验载荷G深度曲线转变成的表征应力G应变曲线与计算曲线进行比较,找到误差最小的一条计算曲线,其对应的材料参数即为要确定材料的实际性能.
2.2 金属材料弹塑性方程
弹塑性方程是反映物质宏观性质的数学模型,可以用来描述每一个应力G应变点的拉伸曲线,而应力G应变点的数学形式取决于其硬化行为.
大部分纯金属和合金的弹塑性行为可以用近似幂指数规律来描述,目前表征应力应变法中普遍采用两参数幂指数方程σ=Kεn 来描述材料的弹塑性行为[4,12].材料的屈服强度由0.2%应变的直线与拟合的真应力G真应变曲线相交得到,由于压痕表征应力超过了其屈服强度,因此屈服强度的预测精度不高.DAO 等采用三参数的改进弹塑性模型来描述真应力G真应变曲线[13],如图3所示,具体公式见式(12).
式中:σy 为材料的屈服强度;εy 为材料屈服时对应的应变.
总的应变ε 由εy 和εp 两部分组成,εp 是屈服 应变εy 之后积累的非线性应变,即
如果把非线性应变εp 定义为表征应变εr[13],即εp=εr,其相应的应力σ则为表征应力σr.因此,表征应力应变法的改进弹塑性方程为

得到n=ln(1+εe)=ε,即当真应变ε=n 时,真应力所对应的工程应力为抗拉强度σu.
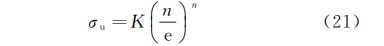
式中:e为自然对数的底,e=2.71828.
2.4 优化条件
将改进弹塑性模型的三个材料参数,即弹性模量E 、屈服强度σy 和应变硬化指数n 作为未知变量,用优选法进行求解.该求解方法保留了表征应力应变法的基本方程,改进了表征应力应变法的优化条件,采用的优化条件是表征应力与模型真应力相应点的误差平方δerror和为最小值.δerror的计算公式为
式中表征应力和模型真应力分别按照式(9)和式(16)求得,表征应变εr 由式(11)求得.
图4 表征应力应变法的计算流程
Fig.4 CalculationflowofrepresentativestressGstrainmethod
2.5 计算流程
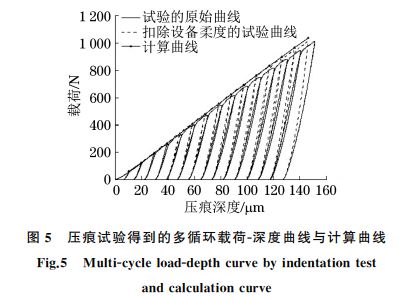
在已有的表征应力应变法中,弹性模量是通过计算卸载曲线的斜率得到的,计算结果的离散性较大;已有表征应力应变法的计算流程中仅对应变硬化指数n 进行迭代优化,并未对屈服强度σy 进行优化.因此,作者利用改进的弹塑性方程对σy、n 和E三个参数同时进行优化,其计算流程如图4所示.采用矩阵实验室 Matlab工具箱 Optimisation中的Lsqnonlin算法对参数进行优化.Lsqnonlin算法即 非线性最小二乘法,只需设定参数的初值及上下限, 便可自动选择优化参数组合并决定下一步的优化方 向,因此可通过自动搜索找出最佳的参数组合. 3 测试应用与结果 3.1 压痕曲线测试结果 采用IITG2000 型压痕仪测载荷G深度曲线,压 痕仪的最大载荷为2000N,位移精度为0.2μm,压 头为直径1mm 的碳化钨球,待检材料为 P91钢. 图5中实线为试验得到的多循环载荷G深度曲 线,包括了 P91钢和设备自身的变形,一共有15个 加载和卸 载 循 环;虚 线 为 扣 除 设 备 自 身 的 柔 度 后 P91钢的载荷G深度曲线;带三角形的实线是优化计 算后得到的载荷G深度曲线,该曲线与图中的虚线几 乎重合,误差很小,这说明优化计算结果与 P91钢 的试验值比较吻合[14].
经 Matlab 优 化 计 算 得 到,当 材 料 屈 服 强 度σy=558MPa,应变硬化指数n=0.0842,弹性模量E=220000 MPa时,这15个表征应力和模型真应力之间的误差最小,如图6所示.图中小黑点代表
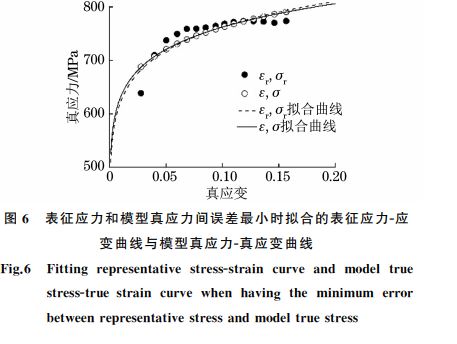
的是从压痕曲线中得到的15个表征应力G应变点,小白圆圈代表的是根据改进的弹塑性方程计算得到的15个模型真应力G真应变点,虚线为表征应力G应变点拟合后的表征应力G应变曲线,实线为根据改进的弹塑性方程得到真应力G真应变点拟合后的模型真应力G真应变曲线,实线为模型真应力G真应变曲线即为材料实际的真应力G真应变曲线.虽然接触边缘剪切应变表达式εr=αtanγ 扩大了表征应变的范围,但是压痕试验需要根据材料布氏硬度的不同而合理选取压入的载荷和深度,避免真应变范围过大,使表征应力G应变曲线和模型真应力G真应变曲线的误差较小.
3.2 球形压痕表征应力应变法测试值和单轴拉伸
试验值的对比
按照 GB/T228.1-2010«金属材料 拉伸试验第1部分:室温试验方法»,采用 CMT5205型电子万能试验机进行单轴拉伸试验.试验材料为 P91钢,拉伸试样的尺寸为?10mm×50mm,试验温度为室温,拉伸速度为1mm??min-1.由表1可以看出,压痕法得到的屈服强度σy、应变硬化指数n、弹性模量E 和抗拉强度σu 与单轴拉伸试验结果的偏差较小,最大偏差值为12.11%.因此,采用压痕法所得到的金属材料力学性能具有较高的精度.
4 结 论
(1)改进了表征应力应变法的优化条件,以表征应力和模型真应力之间的误差值作为收敛条件,使表征应力G应变曲线更接近于模型真应力G真应变曲线.
(2)优化了表征应力应变法的计算流程,并利用改进的弹塑性方程对σy、n 和E 三个参数同时进行优化,从而确定材料的力学性能参数.
(3)球形压痕表征应力应变法测得的 P91钢的力学 性 能 结 果 与 单 轴 拉 伸 试 验 结 果 的 偏 差 较小,最大偏 差 值 为 12.11%,采 用 球 形 压 痕 表 征 应力应变法所得到的金属材料力学性能具有较高的精度.


