分享：汽轮机用3.5NiCrMoV钢和20Cr13钢的非对称应变疲劳行为与寿命预测

吴海利

(上海电气电站设备有限公司,上海200240)

摘 要:对汽轮机用3.5NiCrMoV贝氏体钢和20Cr13马氏体钢进行对称和非对称应变控制疲劳试验,对比研究其疲劳行为;采用基于对称应变疲劳参数的 Morrow模型、SWT模型和Ellyin模型对非对称疲劳寿命进行预测,讨论模型的适用性。结果表明:3.5NiCrMoV钢的非对称疲劳寿命不高于对称疲劳寿命,20Cr13钢的非对称疲劳寿命高于对称疲劳寿命;3.5NiCrMoV 钢的对称和非对称循环应力相差较大,而20Cr13钢的对称和非对称循环应力相近;平均应力下降是非对称应变控制疲劳的共同现象,塑性应变变化是影响非对称疲劳寿命的主要因素;Morrow模型预测精度取决于应变比对疲劳寿命的影响,SWT模型不适用于非对称与对称疲劳循环应力-应变曲线相差较大的3.5NiCrMoV钢疲劳寿命预测,Ellyin模型对非对称与对称循环硬化趋势相近的20Cr13钢的非对称疲劳寿命具有较好的预测效果。

关键词:非对称应变疲劳;平均应力;应变比;寿命预测;汽轮机用钢中图分类号:TB114.3 文献标志码:A 文章编号:1000-3738(2021)09-0045-06

0 引 言

在汽轮机组启动、调峰、停机等不同运行阶段,其机组部件承受非对称循环载荷。由于在高应力范45吴海利:汽轮机用3.5NiCrMoV钢和20Cr13钢的非对称应变疲劳行为与寿命预测围内材料已进入塑性变形状态,应力不再是最有意义的量[1],因此研究其应变控制的疲劳行为显得尤为重要。许多学者开展了低周疲劳寿命可靠性理论研究,提出了很多寿命预测公式和寿命可靠性模型。工 程 上 应 用 较 多 的 对 称 疲 劳 寿 命 模 型 是MANSON[2]和 COFFIN[3]提出的 Manson-Coffin方程。在非对称疲劳寿命预测方面:MORROW[4]提出在 Manson-Coffin方程的基础上进行平均应力修正;SMITH 等[5]综合考虑拉力分量作用下单轴应力和应变的影响提出了在 Manson-Coffin方程引入最大应力和应变幅乘积作为损伤因子的SWT方程;ELLYIN等[6]考虑平均应力效应的影响提出了总循环应变能密度理论。目前,学者们已经对汽轮机材料开展了很多低周疲劳试验,并积累了大量对称应变疲劳的基础试验数据。近年来在非对称应变疲劳行为方面也开展了相应研究,例如:张孝忠等[7]对汽轮机长叶片材料开展了应变比R 为0的非对称低周疲劳试验,建立了一种考虑平均应力松弛的叶根低周疲劳寿命预测方法;吴德龙[8]对汽轮机转子材料高铬钢进行了600℃对称和非对称应变疲劳试验,建立了与应变幅相关的循环软化和平均应力松弛行为预测模型;还有一些学者对比了不同应变比下其他工程材料的非对称疲劳循环曲线和循环寿命[9-11]。非对称疲劳行为相对复杂,且寿命预测模型的适用性研究也较少。为充分理解非对称应变疲劳力学响应特征,选用典型汽轮机用贝氏体基体转子钢3.5NiCrMoV和马氏体基体叶片钢20Cr13进行对称和非对称应变控制疲劳试验,对其对称和非对称应变疲劳试验数据进行对比分析,采用基于对称应变疲劳参数的寿命模型对非对称疲劳寿命进行估算,讨论模型的适用性。

1 试样制备与试验方法

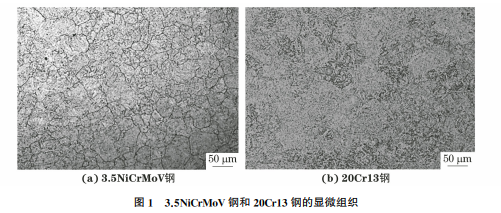
试验材料包括典型汽轮机转子用3.5NiCrMoV钢和叶片用20Cr13钢,2种试验钢的显微组织如图1所示,其中:3.5NiCrMoV钢的基体组织为贝氏体,屈服强度为650MPa,抗拉强度为780MPa,弹性模量为230GPa;20Cr13钢的基体组织为马氏体,屈服强度为674MPa,抗拉强度为818MPa,弹性模量为219GPa。图1 3.5NiCrMoV钢和20Cr13钢的显微组织Fig 1 Microstructuresof3 5NiCrMoVsteel a and20Cr13steel b按照 GB/T15248—2008,采用 MTS810型电液伺服疲劳试验机进行对称和非对称应变控制疲劳试验。疲劳试样为等截面圆柱试样,直径为8mm。控制方式为轴向应变控制,试验波形为三角波,应变速率为4×10-3s-1,试验温度为(23±2)℃。对称循环 下 的 应 变 比 Rε 为 -1,3.5NiCrMoV 钢 和20Cr13钢在非对称循环下的应变比Rε 分别为0,0.05,应变幅Δεt/2均为0.002~0.015。

2 试验结果与讨论

2.1 对称与非对称疲劳试验

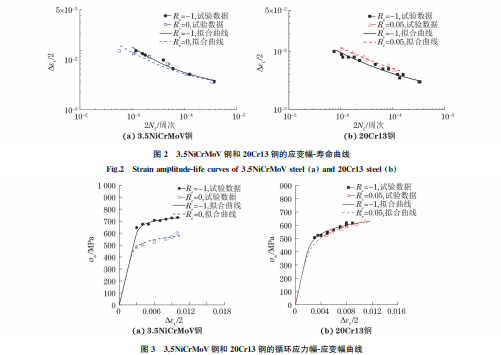
数据的对比由图 2 可 知:在 应 变 幅 为 0.006,0.008 下,3.5NiCrMoV钢在Rε 为-1时的对称疲劳寿命Nf与Rε 为0时的非对称疲劳寿命相近,在其余应变幅下Rε 为0时的非对称疲劳寿命均低于Rε 为-1时的对称疲劳寿命;20Cr13钢在Rε 为0.05时的非对称疲劳寿命均高于Rε 为-1时的对称疲劳寿命。由图3可知:在相同应变幅下,3.5NiCrMoV钢在Rε 为0时的应力幅σa 远低于Rε 为-1时的应力幅,相差近200MPa;而20Cr13钢在Rε 为0.05时的应力幅与Rε 为-1时的相近

2.2 非对称疲劳平均应力

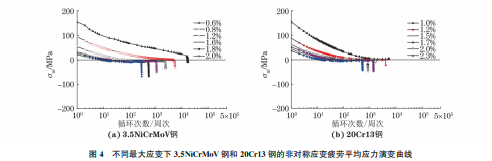
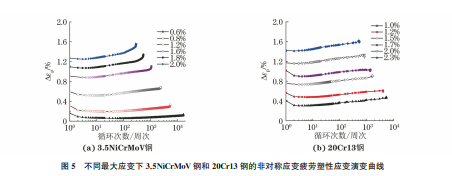
演变过程由图4可知:3.5NiCrMoV钢和20Cr13钢的非对称疲劳平均应力σm 演变过程相似,当最大应变较小时,初始平均应力较高,在循环过程中平均应力46吴海利:汽轮机用3.5NiCrMoV钢和20Cr13钢的非对称应变疲劳行为与寿命预测逐渐下降并趋于0;随着最大应变的增大,初始平均应力降低,在循环初期下降速率较快,经数十次循环后平均应力降至0,然后进一步降至负值,最后保持平稳直至失效。图2 3.5NiCrMoV钢和20Cr13钢的应变幅-寿命曲线Fig 2 Strainamplitude-lifecurvesof3 5NiCrMoVsteel a and20Cr13steel b图3 3.5NiCrMoV钢和20Cr13钢的循环应力幅-应变幅曲线Fig 3 Cyclicstressamplitude-strainamplitudecurvesof3 5NiCrMoVsteel a and20Cr13steel b图4 不同最大应变下3.5NiCrMoV钢和20Cr13钢的非对称应变疲劳平均应力演变曲线Fig 4 Asymmetricalstrainfatigueaveragestressevolutioncurvesof3 5NiCrMoVsteel a and20Cr13steel b underdifferentmaximumstrains由图5可知,随着最大应变的增大,初始塑性应变Δεp 增加。3.5NiCrMoV钢在较小最大应变下的塑性应变增长缓慢,而在较大最大应变下的塑性应变增长迅速。20Cr13钢在不同最大应变下的塑性应变增加速率相对恒定,在最大应变εmax 为1.2%,1.7%,2.0%的疲劳末期出现了塑性应变降低的现象。在循环过程中塑性应变 Δεp 不断累积[12],应变循环回复到最小应变时需要提供更大的压应力,拉 应 力 与 压 应 力 的 相 对 差 值 减 小,导 致3.5NiCrMoV钢和20Cr13钢的非对称应变疲劳平均应力降低。在小应变幅下试验钢中产生的初始塑性应变较小,此时拉应力远大于压应力,初始平均应力较大;随着应变幅的增大,初始塑性应变增加,拉/压应力差值减小,在较少循环次数下平均应力趋于0。3.5NiCrMoV钢和20Cr13钢均为循环软化材料,循环过程中拉应力降低,同时塑性应变累积增加,压应力逐渐超过拉应力,平均应力表现为负值并保持稳定直至失效。47吴海利:汽轮机用3.5NiCrMoV钢和20Cr13钢的非对称应变疲劳行为与寿命预测图5 不同最大应变下3.5NiCrMoV钢和20Cr13钢的非对称应变疲劳塑性应变演变曲线Fig 5 Asymmetricalstrainfatigueplasticstrainevolutioncurvesof3 5NiCrMoVsteel a and20Cr13steel b underdifferentmaximumstrains在小应变幅条件下,3.5NiCrMoV 贝氏体钢中位错滑移被贝氏体晶界钉扎所阻碍,塑性应变较小并平稳增长。在大应变幅条件下,贝氏体组织的滑移线快速增殖,加速了材料损伤,引发的群体短裂纹降低了材料的有效抗载能力[13],导致疲劳过程中塑性应变快速增长,疲劳寿命明显降低。20Cr13马氏体钢在循环过程中其马氏体板条逐渐粗化,形成等轴亚晶结构,晶内位错密度降低[8,14],这在一定程度上缓释了塑性变形,因此在疲劳过程中塑性应变增加速率恒定,疲劳寿命增加。综上可知,平均应力下降是非对称应变控制疲劳的共同现象,下降的幅度和速率与应变幅直接相关。在平均应力下降的条件下,2种基体组织材料的非对称疲劳寿命相对于其对称疲劳寿命分别呈现增加和降低两种相反结果,可知平均应力下降对疲劳寿命没有必然影响,而由基体组织损伤机制导致的塑性应变变化是影响非对称疲劳寿命的主要因素。

3 非对称疲劳寿命预测

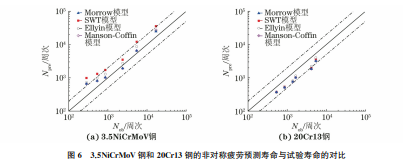
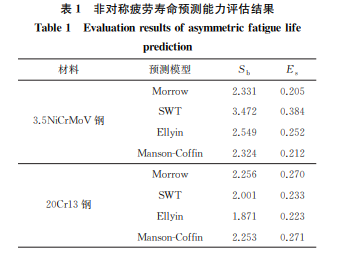
使用 Manson-Coffin[2-3]模型拟合对称应变控制疲劳 数 据,获 取 3.5NiCrMoV 钢 和 20Cr13 钢 的Manson-Coffin拟合参数。Manson-Coffin模型为Δεt2=σ'fE(2Nf)b +ε'f(2Nf)c (1)式中:σ'f 为疲劳强度系数;b为疲劳强度指数;ε'f 为疲劳延性系数;c为疲劳延性指数;E 为弹性模量;Δεt 为总应变范围。在对称疲劳参数的基础上通过修正或引用而建立的非对称疲劳模型包括以下3组公式。(1)Morrow平均应力修正公式[4],其表达式为Δεt2=σ'f -σmE(2Nf)b +ε'f(2Nf)c (2)(2)SWT公式[5],其表达式为σmaxΔεt2=(σ'f)2E(2Nf)2b +σ'fε'f(2Nf)b+c (3)式中:σmax 为循环最大应力。(3)Ellyin总应变能密度公式[6],其表达式为ΔWt=Au(2Nf)γ (4)ΔWt=ΔWe+ΔWp (5)ΔWe=12EΔσ2 σm2(σmin ≤0)(σmax-σmin)22E(σmin ≥0)??????????????(6)ΔWp=∫Δσdεp=1-n'1+n'ΔσΔεp (7)式中:ΔWt 为总应变能密度;ΔWe 为弹性应变能密度;ΔWp 为塑性应变能密度;Δσ 为应力范围;n'为循环应变硬化指数;Au 为拟合系数;γ 为拟合指数;σmin 为循环最小应力。使用上述3种非对称疲劳预测模型和 MansonCoffin 对 称 疲 劳 预 测 模 型 对 3.5NiCrMoV 钢 和20Cr13钢的非对称疲劳寿命进行预测,预测寿命Npre 与试验寿命 Nob 的对比结果如图6所示。预测寿命与试验寿命的偏离程度用分散带Sb 和标准差Es 表示[11],分散带和标准差越小,表明预测寿命与试验寿命的偏差越小,预测精度越高。分散带和标准差的计算公式分别为Sb=max(Nob/Npre,Npre/Nob) (8)Es=1n-1∑ni=1??(lgNpre-lgNob)2??????????????1/2(9)式中:n为数据点数量。由表1可知,Morrow模型与 Manson-Coffin模型的预测结果基本相同,预测寿命与试验寿命的分散带均超过2。3.5NiCrMoV 钢和20Cr13钢的非对称疲劳平均应力均趋于0,对Morrow公式的修48吴海利:汽轮机用3.5NiCrMoV钢和20Cr13钢的非对称应变疲劳行为与寿命预测图6 3.5NiCrMoV钢和20Cr13钢的非对称疲劳预测寿命与试验寿命的对比Fig 6 Comparisonbetweenpredictionasymmetricfatiguelifeandtestfatiguelifeof3 5NiCrMoVsteel a and20Cr13steel b正作用很小;Morrow 模型预测精度取决于应变比对材料疲劳寿命的影响程度。3.5NiCrMoV钢的非对称和对称疲劳循环应力-应变曲线差别较大,导致SWT模型预测寿命与试验寿命间有较大的偏差,预测寿命与试验寿命的分散带为3.472;20Cr13钢的非对称和对称疲劳循环应力-应变曲线相近,其SWT模型的预测寿命偏差相对较小,预测寿命与试验寿命的分散带为2.001。Ellyin总应变能密度公式引入了平均应力修正和对称疲劳的硬化指数,其中平 均 应 力 修 正 效 果 可 忽 略。Ellyin 模 型 对3.5NiCrMoV钢 非 对 称 疲 劳 寿 命 的 预 测 效 果 在Morrow模型和 SWT 模型之间,而 20Cr13 钢的Ellyin模型预测寿命的分散带小于2,标准差相对最小。由此可知,Ellyin模型对20Cr13钢非对称疲劳寿 命 的 预 测 效 果 较 好。由 图 3 可 以 看 出,3.5NiCrMoV钢的对称与非称循环硬化趋势相差较大,而20Cr13钢的对称与非对称循环硬化趋势相似。表1 非对称疲劳寿命预测能力评估结果Table1 Evaluationresultsofasymmetricfatiguelifeprediction材料 预测模型 Sb EsMorrow 2.331 0.2053.5NiCrMoV钢SWT 3.472 0.384Ellyin 2.549 0.252Manson-Coffin 2.324 0.212Morrow 2.256 0.27020Cr13钢SWT 2.001 0.233Ellyin 1.871 0.223Manson-Coffin 2.253 0.271综上可知:对于平均应力趋于0的非对称应变疲劳寿命预测,基于修正平均应力的 Morrow 模型与对称疲劳 Manson-Coffin模型的预测效果基本相同,其预测精度取决于应变比对疲劳寿命的影响;基于力学参量的SWT模型不适用于非对称与对称疲劳循 环 应 力-应 变 曲 线 相 差 较 大 的 贝 氏 体 基 体3.5NiCrMoV钢的非对称疲劳寿命预测;Ellyin模型对循环硬化趋势相近的20Cr13钢的非对称疲劳寿命具有较好的预测效果。

4 结 论

(1) 在 相 同 应 变 幅 下,贝 氏 体 基 体3.5NiCrMoV钢的非对称疲劳寿命不高于对称疲劳寿命,马氏体基体20Cr13钢的非对称疲劳寿命高于对称 疲 劳 寿 命;在 相 同 应 变 幅 下,贝 氏 体 基 体3.5NiCrMoV钢的对称和非对称循环应力相差较大,而马氏体基体20Cr13钢的对称和非对称循环应力相近。(2)平均应力下降是非对称应变控制疲劳的共同现象,下降的幅度和速率与控制应变幅直接相关。平均应力下降对疲劳寿命没有必然影响,由基体显微组织损伤机制导致的塑性应变变化是影响非对称疲劳寿命的主要因素。(3)3.5NiCrMoV 钢和20Cr13钢的非对称疲劳平均应力均趋于0,基于修正平均应力的 Morrow模型与对称疲劳 Manson-Coffin模型的疲劳寿命预测效果基本相同,其预测精度取决于应变比对疲劳寿命的影响。基于力学参量的SWT模型不适用于非对称与对称疲劳循环应力-应变曲线相差较大的贝氏 体 基 体 3.5NiCrMoV 钢 的 疲 劳 寿 命 预 测。Ellyin模型对非对称与对称循环硬化趋势相近的20Cr13钢的非对称疲劳寿命具有较好的预测效果。

来源：材料与测试网