分享:极射投影法与极图的演变过程及其应用
摘要: 极射投影法是直观的三维方向关系表达法,极射投影图使其变为二维面上的关系。极图除含极射投影的含义外,还包含样品坐标系的信息,涉及样品坐标系的取向或方位,即需要标出晶体坐标系相对于样品坐标系的旋转关系。在晶体学、形变、再结晶及相变等知识的认知学习中使用了用于描述材料内部晶体学方向分布关系或规律的极射赤面投影法与极图,材料科学研究中涉及晶体学理论、现象与规律时常常用到这些图。学生初次学习很难体会到它们有多大的用途并且普遍认为这是个认知难点,而极射赤面投影图与极图两个概念也常常相互混淆。本文从极射赤面投影基本概念入手,介绍了极射投影法的演变历史、相关科学人物故事以及其在数学、几何学、绘图、地质学、摄影技术中的应用,希望有助于分清极射投影图与极图两者的相似处与不同点。通过极射投影图在教学中的应用举例,进一步介绍了极射投影图与极图在材料科学中的应用,达到有针对性解决问题,希望不仅对普通读者,也对初次接触这种方法的研究人员能有所帮助。
晶体学涉及晶体本身的性质(如对称性和各向异性)及晶体在外部条件变化时的结构变化(如温度、压力、磁场、电场等)。描述晶体本身及其变化的最常用的工具之一就是极射赤面投影法或极射投影图。《材料科学基础》课程是材料专业最基本的理论课程,涉及的材料主要是晶体。如果问刚学过《材料科学基础》课程的学生,哪些概念相对难?苦涩难懂?肯定会有不少同学说,极射投影图难懂,有效使用更难。如果问及这个工具用于哪些场合?同学们基本能答出用于确定不同晶体学方向夹角的测定,用于多晶织构的表达。至于熟练应用,就很难达到,或令人望而生畏了。针对此现象,作者曾编辑出版了《材料科学名人典故与经典文献》[1]一书,收集整理了极射投影图方法的演变历史及在不同领域的应用,并在课程教学中予以展示。由于作者长期从事的材料学研究中频繁用到极射投影图和极图,因此充分体会到其直观性和便利性;此外,随着科技的不断进步,特别是计算机及软件开发和测试技术的进步,晶体学这个既传统又成熟但其应用还远不普及的学科,越来越频繁地被应用,极射投影图也越来越广泛地得以使用。在此结合作者所收集的资料和自己的科研工作讨论极射投影法和极图的“神奇”、有趣和广泛应用,希望引起读者的兴趣,并在研究工作中注重其应用。
1. 极射赤面投影的基本概念
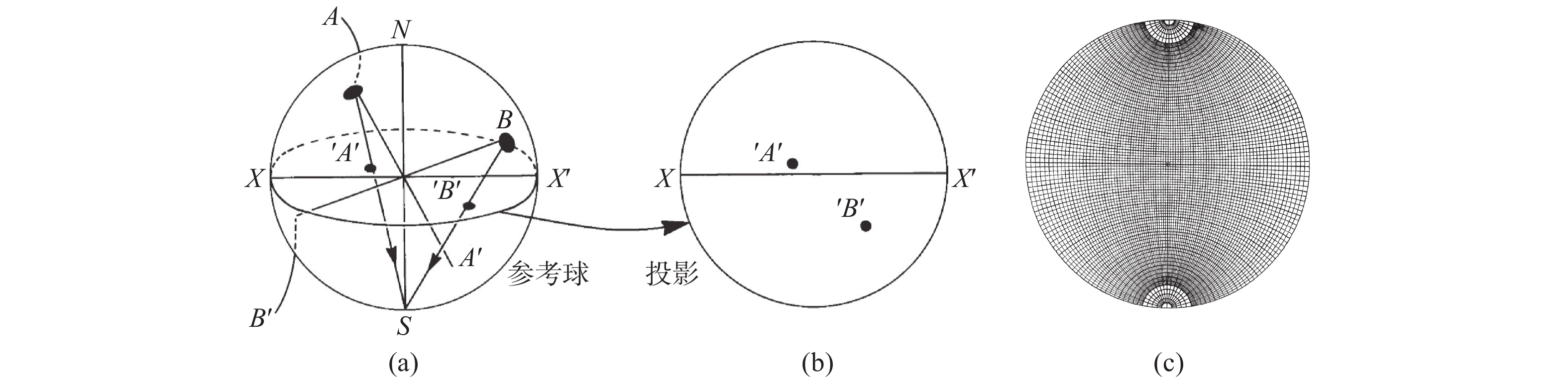
图1给出极射赤面投影原理图。极射赤面投影方法是由单位球的中心出发的任一晶向,与球面相交(球面投影概念)于A点,该交点A向单位球的南极(下半球)投影,投影线AS与赤道面的交点′A′就是该晶向三维方向的二维坐标或表达。类似地可做出三维晶体方向B(实际是原点到B的方向)在二维赤道面的投影位置′B′。A,B方向在空间的夹角就等于′A′和′B′在平面投影图中的夹角,该投影过程是保角的,这个角度要用吴氏网(Wullf net)来度量,见图1(c)。具体方法是,将′A′ 、′B′投影点转到吴氏网的经线上,量出它们之间的纬度角值。由极射赤面投影制作过程及使用的吴氏网可知,极射赤面投影图与地球仪、地理、航海有密切联系,甚至可以说是由其演变而来。吴氏网上的经线是不同倾斜角度并过球心的大圆的极射投影,而吴氏网上的纬线是垂直于赤道面的一系列小圆的极射投影线。
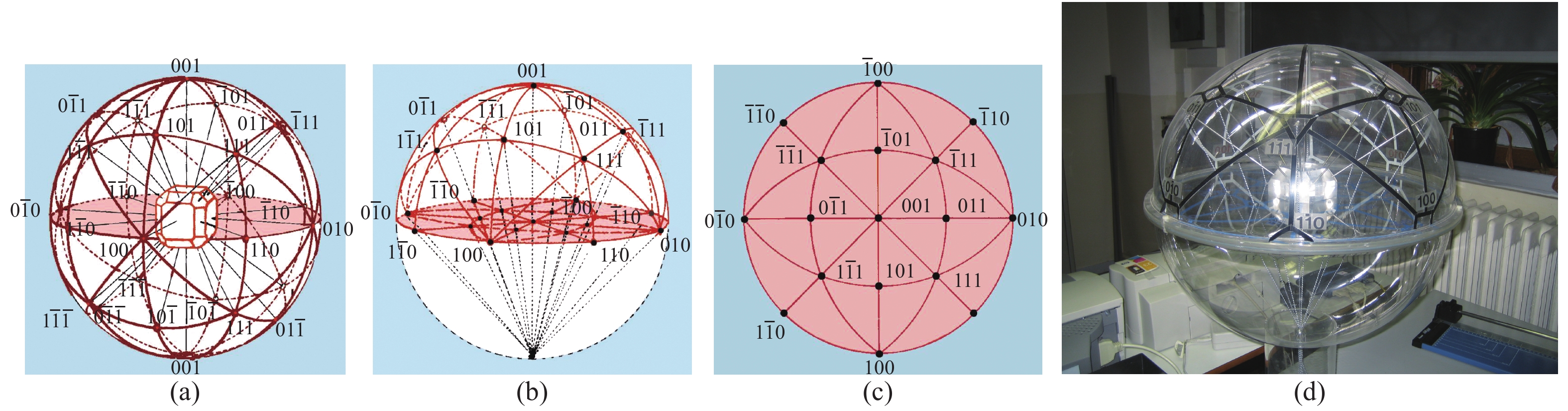
在晶体学中,为了一目了然地看出晶体中所有重要晶面的相对取向及对称关系,通常使用的方法是制作极射赤面标准投影图。一般选择某个低指数晶面(例如(100)、(110)、(111)等)作为投影面(即赤道面),将其他重要的晶面的极点投影到这个面上(图2(c))。图2是立方系(001)标准投影图的制作过程及其标准投影图。能看出绕中心<001>轴的4次对称性及镜面对称关系。图2(d)是作者2005年在比利时鲁汶参加国际材料织构会议参观鲁汶大学材料学院时见到的极射投影法教具,是图2(b)的实物化。如果要求出极射图(图2(c))中某一位置点对应哪个(hkl)晶向指数是多少?只需量出其与3个<100>轴的交角,求出3个角度余弦之比并互质化即可[2]。反之,如果要确定一个(hkl)极点或晶向在标准投影图中的位置,只需求出其与三个{100}晶轴的夹角,在极射投影图中画出对应角度的大圆及两个纬线,其惟一的交点就是(hkl)极点位置。
在学习极射投影法时,应注意区分极射投影图与极图的差异。极图是在讲述形变织构、再结晶织构知识点时使用的术语。不了解织构的人可能认为极图就是极射投影图的缩写,其实极图除含极射投影的含义外,还包含样品坐标系的信息,即标出晶体坐标系相对于样品坐标系的旋转关系(这就是晶体取向的定义),{100}极图指画出所有不同取向晶粒的{100}投影点、又表达出样品坐标系与晶体坐标系旋转关系的极射投影图(见后文的举例)。很多情况下,使用者不关心样品坐标系,只关心晶体坐标系,因此就用常见的极射投影图。而一旦涉及样品坐标系的取向或方位,就要用极图。
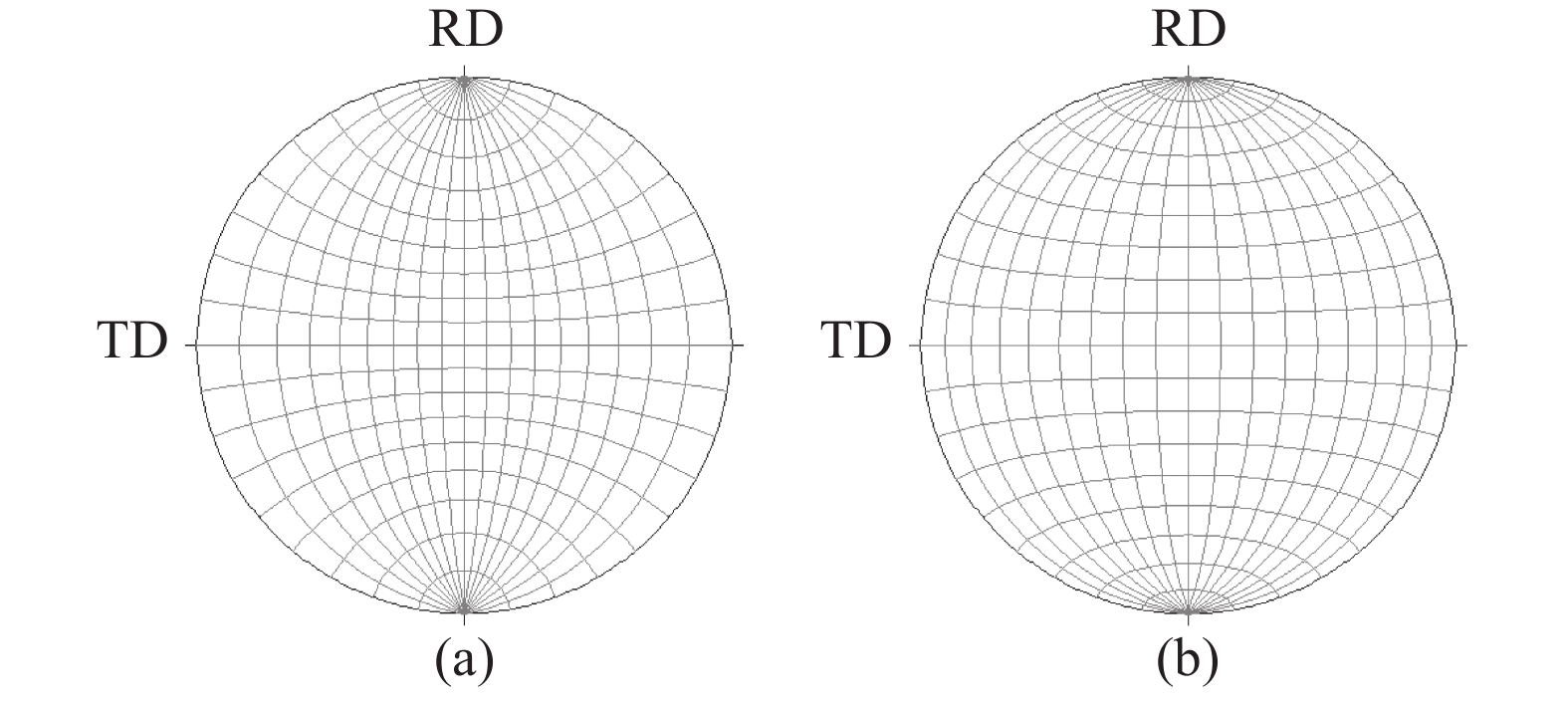
不同领域的研究者还应注意极射投影法与等面积投影法的差异[3]。矿物学、晶体学中主要分析各种晶体学方向或晶面间的关系,要在二维图上保持三维空间的角度关系,所以习惯使用等角度投影的吴氏网(Wullf net)来度量;而地质学、地理学、测绘学中常需要描述地球上不同区域或国家大小比例间的关系,所以习惯用等面积投影的方式作图或度量,这就要用到等面积投影的Lambert网或Schmidt网[4]。图3给出(a)等角度投影吴氏网(Wullf网)与(b)等面积投影Schmidt网的差异。绘制两种网的数学公式的差异见文献[3]。
2. 极射赤面投影法应用历史
2.1 极射投影图的历史演变
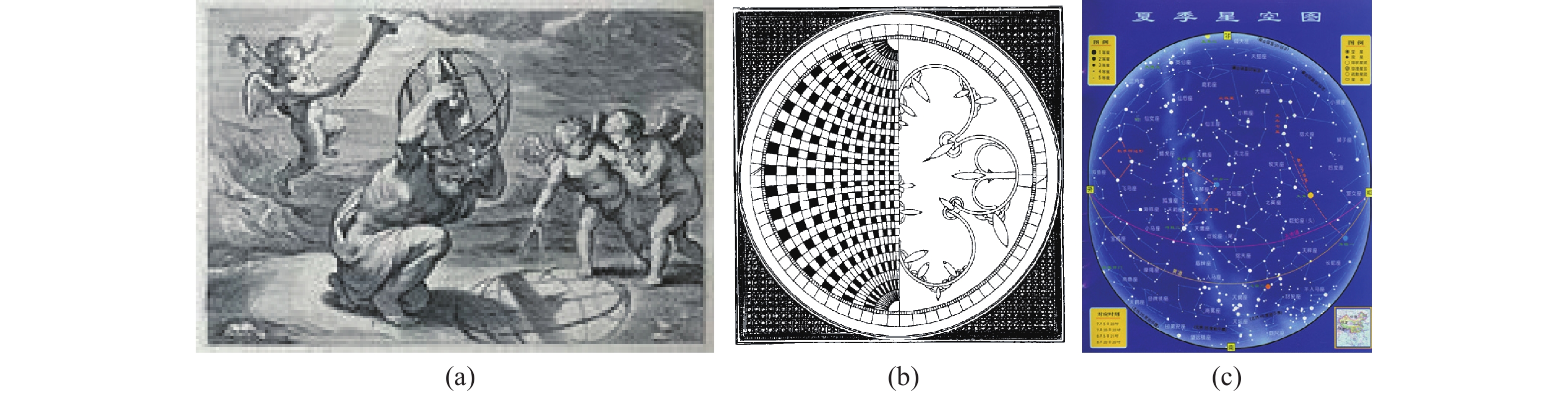
由构造极射赤面投影图时提到的南极、北极、赤道,就不难想象,这种方法是从地理学演变过来的。然而在天体学中极射投影法的应用比地理学还早。早在公元前125年,古代最伟大的天文观察家、三角几何学的开创者Hipparchos(希帕克斯)最先引入极射投影法[3],大致出现在古埃及时代,最初称为平面球形投射。托勒密(Ptolemy)的“星图”(Planisphaerium)是现存文献中最早描述极射投影的著作(参见
作者曾有集邮的爱好,留学德国期间也收集了一些德国的邮票,恰好有一套1500—1700年收藏家所拥有的天体仪与地球仪藏品的邮票,见图5。天体仪可以用于确定宇宙中各星球的相对位置,也可用于确定24个节气和每天24小时的时间点。
天体仪是天体定位的工具,是指一个以地球质心M为中心,半径r为任意长的一个假想的球体。其目的是将天体沿观测者视线投影到球面上(球面投影的概念),以便于研究天体及其相互关系。有时还将天球球心设置在某些特殊点,如地心和日心,相应的天球分别称为地心天球和日心天球。天文航海按自身的需要,把地心作为天球的球心。星星从东方的地平线爬上来,爬到最高点(中天),然后往西方沉下去。看起来就像整个天球围绕着地球旋转一样。古时候人们为了辨别方向、确定时间,创造出日晷和圭表来。古代天文学家为了测定星星的方位和运动,又设计制造了许多天体测量的仪器。通过对星空的观察,将星空划分成许多不同的星座,并编制了星表。通过对天体的测量和研究形成了早期的天文学。直到16世纪中叶,哥白尼提出了日心体系学说,从只是单纯描述天体位置、运动的经典天体测量学,发展成寻求造成这种运动力学机制的天体力学。
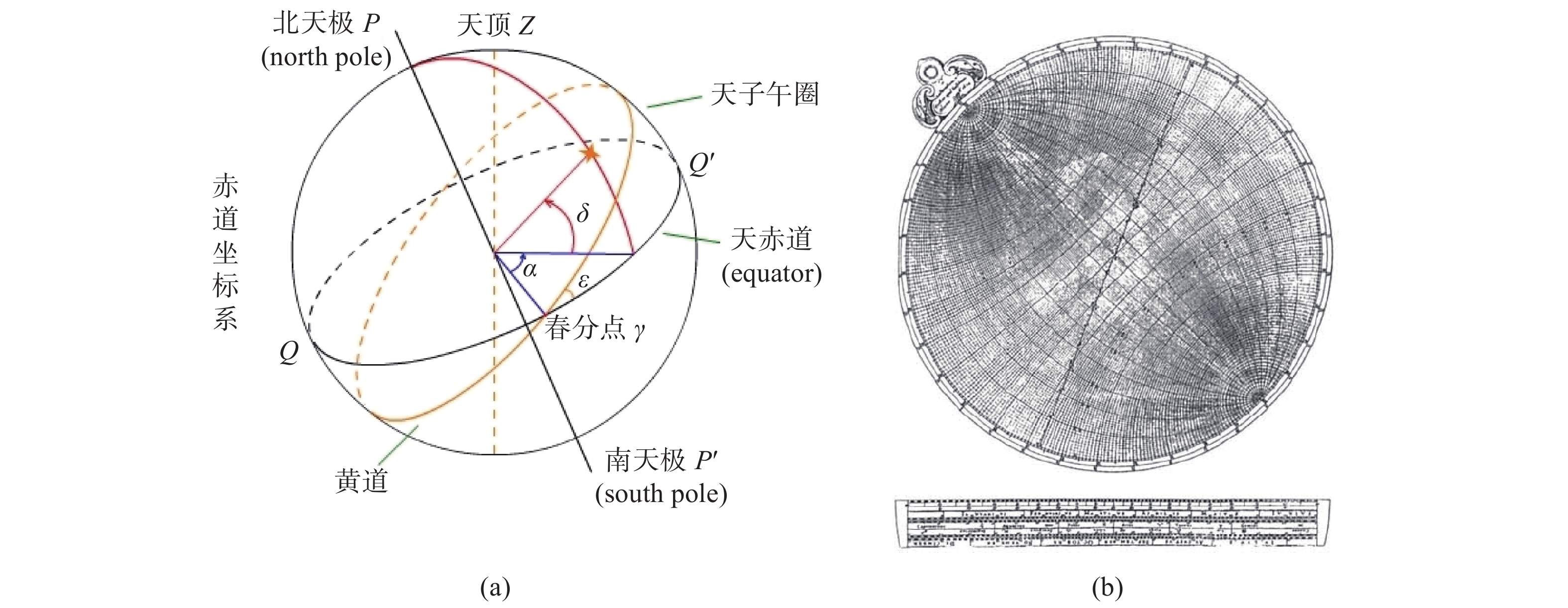
天球坐标系中有几种不同的坐标表达方式(参见
1823年F.E. Neumann最先将极射投影网用于矿物学[3]。1892年俄罗斯的晶体学家Federov因发明了万用测角显微镜台和1902年Wullf网的引入而共同推广了其使用,见图7。
最早的织构在极图(这时同时涉及样品坐标系与晶体坐标系)上的表示:德国柏林大学的Wever于1924年用极图表示了用X射线劳厄照相法获取的轧制铝和轧制铁的织构信息[5]。
图8是2012年诺贝尔化学奖得主、以色列的材料学家Shechtman1982年发表准晶文章中使用极射投影图表示的5次旋转反演对称性(经典的晶体只有1、2、3、4、6次轴对称性)[6]。
简而言之,极射投影法最早在天体学中应用,随后在航海、制图学和测量学中的应用,然后才用于矿物学和晶体学以及地质学中,此外也在数学、摄影学等领域应用。
2.2 极射投影技术的相关人物
与晶体学(含矿物学与材料科学)领域使用极射投影技术相关的人物除了俄罗斯的费德洛夫(Fedorov)、英国的布拉格(Bragg)父子外,这里仅介绍使用极射投影网的两位人物,俄罗斯的吴尔夫(Wulff)和奥地利的施密特(Schmidt),两种投影图网格工具以他们的名字命名。
俄罗斯矿物学家、莫斯科国家大学教授乔治?吴尔夫(Georgii Yuri Viktorovich Wulff (1863—1925))不是最早使用Wullf网的,而是他于1902年最早制作了最高“分辨率”的Wullf网,即直径20 cm、每隔2°一个格。吴尔夫(照片见图9,参见
极射投影法测量的另一个代表人物是奥地利地质学家和岩相学家Walter Schmidt(1885—1945,参见
3. 极射投影法的应用
以下简单介绍极射投影法在各领域的广泛应用(参见
3.1 在不同学科中的应用
3.1.1 在数学、几何学中的应用
(1)用于复变函数;(2)用于线和平面3维的可视化;(3)用于多面体的可视化;(4)用于算法几何。
3.1.2 在绘图中的应用(Cartography)
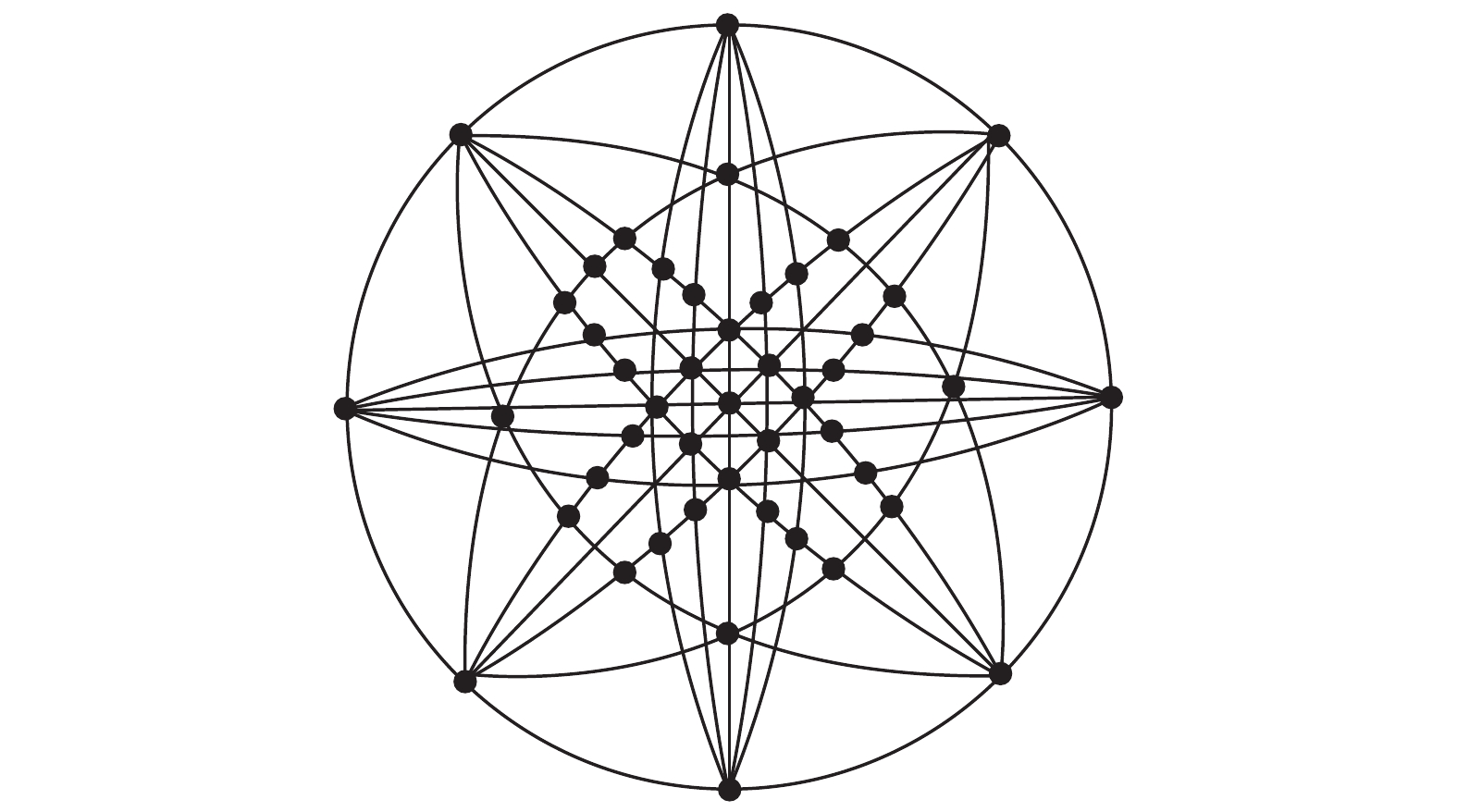
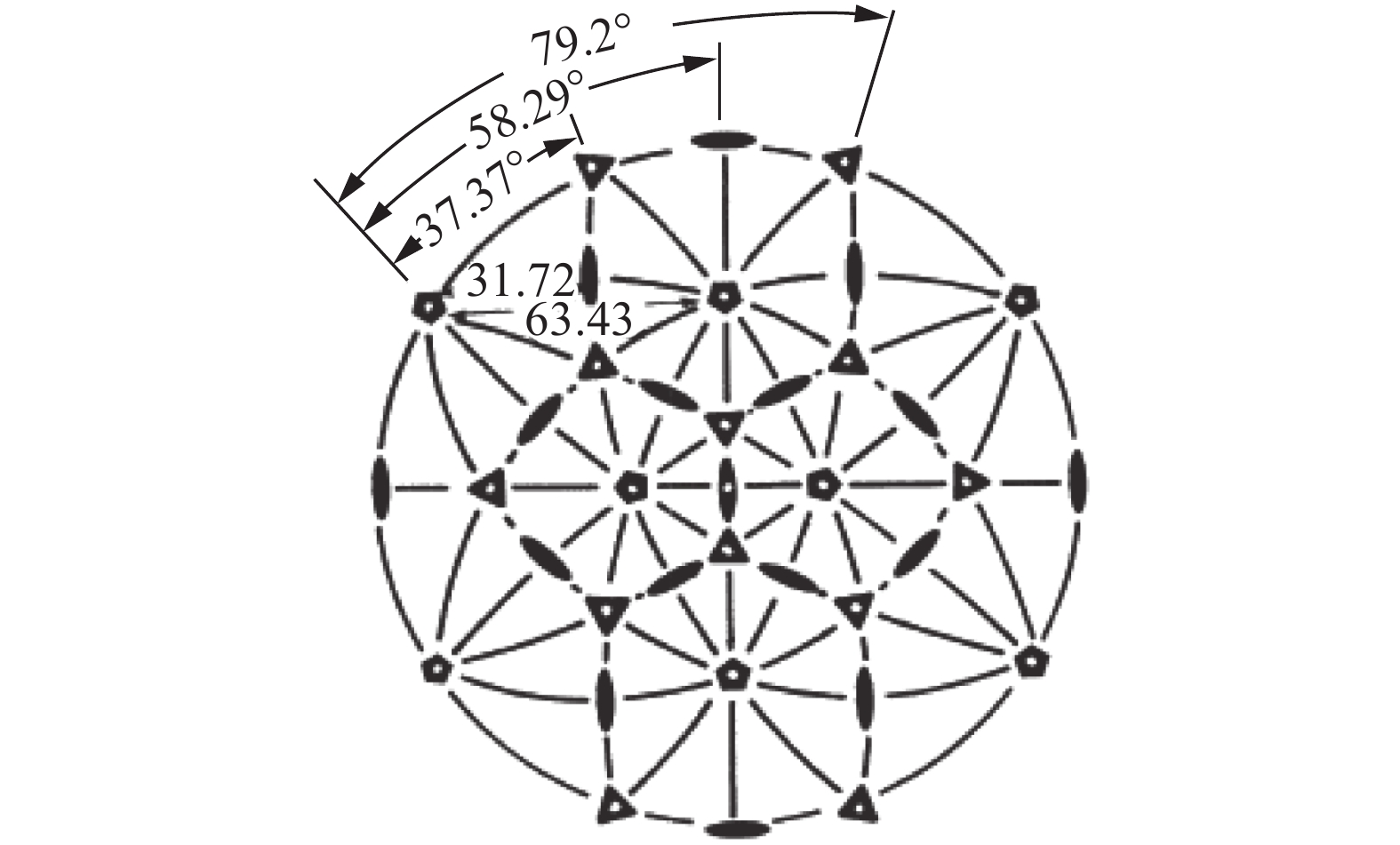
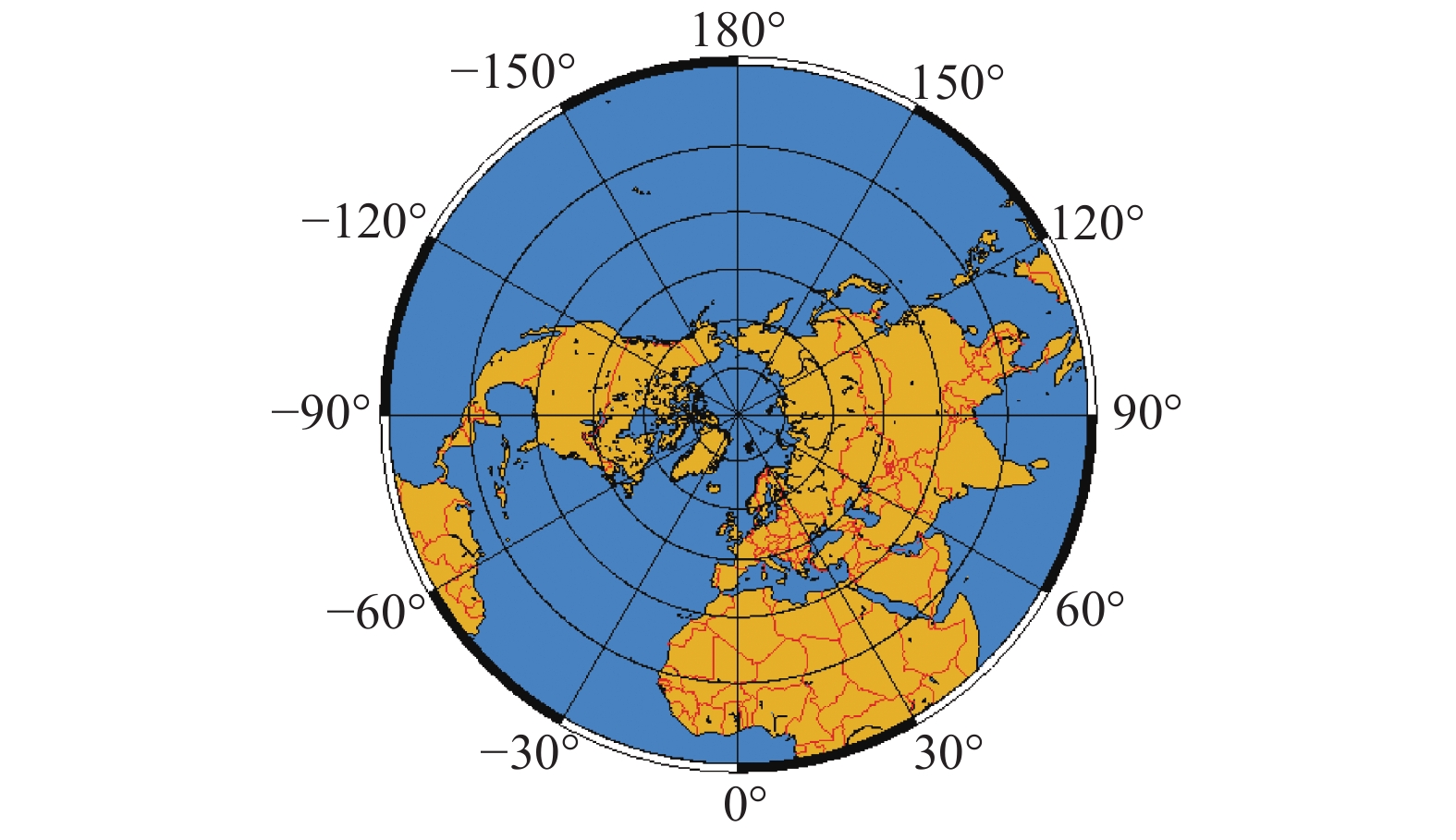
极射投影可用于映射地球。一般来说,统计方面应用更倾向于使用保面积映射投影,因为他们在积分学上有很好应用;而用于导航时则更倾向于使用保角映射投影。当投射集中在地球的北极或南极时,它将有额外的特性,即将经线表示成过原点到圆周的射线上,将纬线表示成集中或环绕于原点的圆周上,见图10。
3.1.3 在地质学中的应用
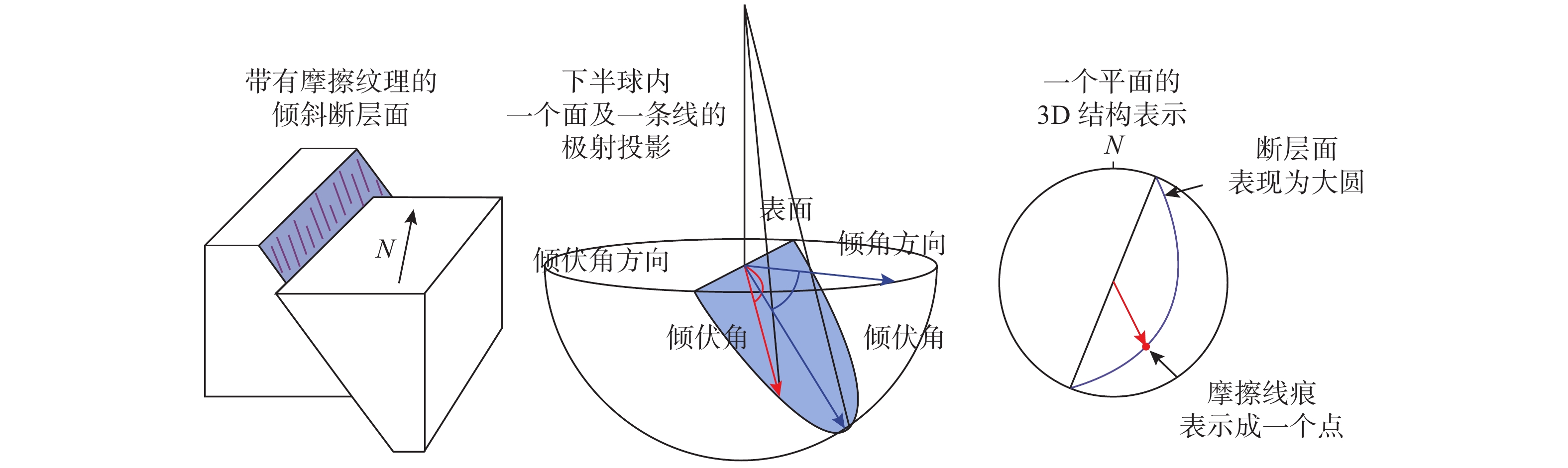
在构造地质学中,应用下半球的极射投影描绘平面和线的取向。人们关注的是岩石的面型特征-摺纹(foliation),而面型特征又由线型特征组成,称为线理(lineation)。比如,面型特征断层面(Fault)包含线型特征是带有岩石间相对摩擦纹理的光滑表面(slickensides),见图11。这些在不同尺度范围内的线和面的取向就可以用上述所说的线和面的显像方法来描绘。与晶体学中使用极射投影相似的是,地质学中的平面也用它的法线(极点)来表示;不同的是,地质学中采用的是南半球而不是北半球(因为人们关注的问题发生在地球表面之下)。
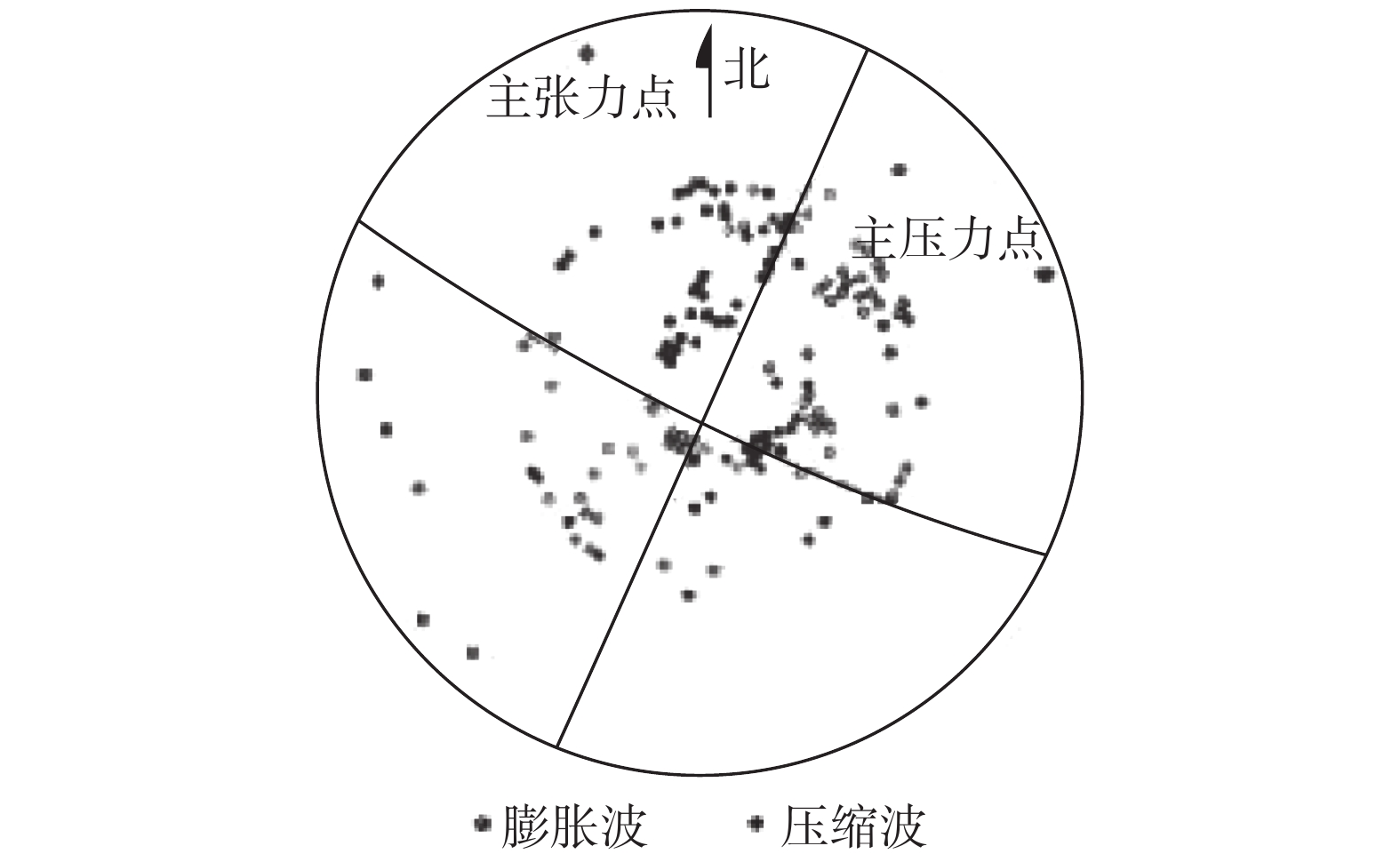
图12是1976年7月28日中国唐山大地震的P波初动符号和震源机制解答参数用吴尔夫网表示的结果(参见
3.1.4 在摄影术中的应用(Photography)
鱼眼镜头利用极射投影方法,以获得更宽的视野(即广角的概念)。利用保角的极射投影的鱼眼镜头优于利用保面积的极射投影,因为保角的极射投影可使接近边缘的区域更好地保留他们的形状,并且直线很少被投影成弯曲线,见图13。
3.2 极射投影图在作者教学中的应用举例
由于本科课程学时有限,课上难以也没有必要展示极射投影的广泛用途,但可以在研究生与晶体学有关课程中进一步介绍。由此作者在研究生“材料结构”课程教材《工程材料结构原理》[7]中编入相应内容。将科研体会放在其中,将小软件送给学生训练加速理解;在企业技术人员的培训中,将各方面应用放在一起比较,培养归纳整理、总结的能力。
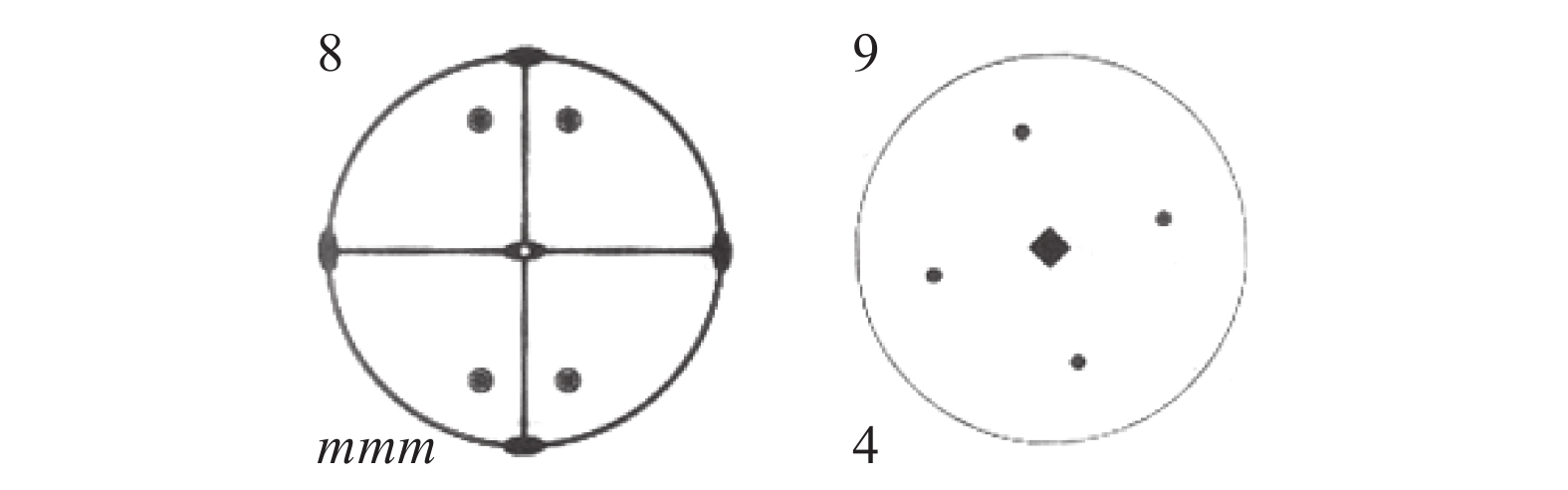
图14为用极射投影图表示晶体学点群对称性特征的例子,是德国晶体学家Hessel提出的32种点群中第8、9号点群在极射图中的表达。
图15(a)是用极射投影图表示闭形单晶外表面相同的{120}等效晶面对称关系及位置的例子。立方晶体中1种闭形的立体形态(五角十二面体)及其极射赤面投影,图15(b)是作者购置的FeS2单晶实物,与图15(a)示意图对应。
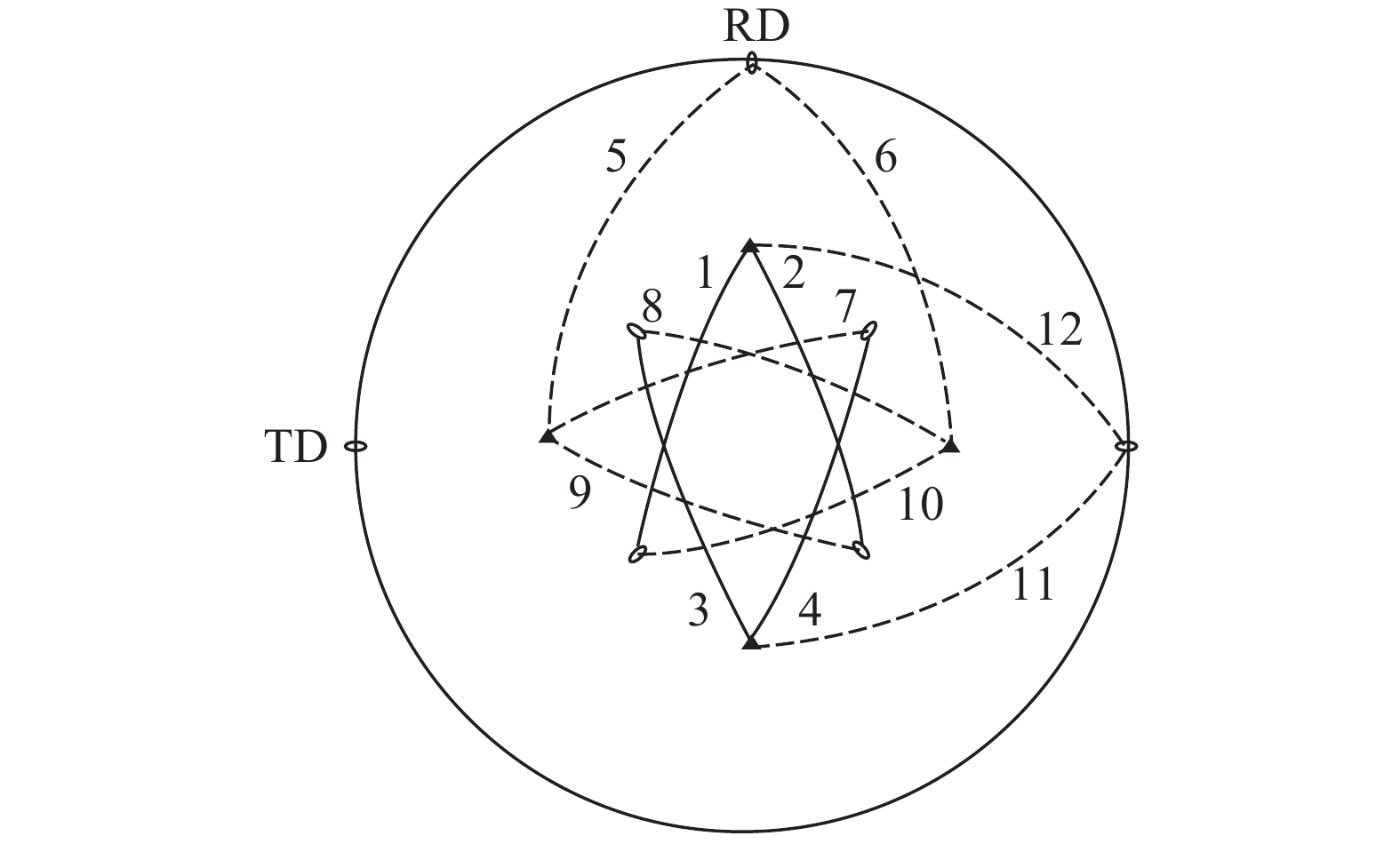
图16为用极射投影图表达晶体塑性形变时不同滑移系开动行为的例子。对应一个{100}<011>取向晶体的12个滑移系,每个滑移系由一个{111}极和{110}极连线组成,两个极连成线。其中4个滑移系取向因子最大而首先开动(图中的实线)。面心、体心立方结构的滑移系位置一样。在极图上讨论取向变化规律。两个滑移系有相同的滑移方向称共向滑移,极图上有相交的{110}点(BCC金属);两个滑移系有相同的滑移面称共面滑移系,在极图上有相交的{111}极点(FCC)。这个几何图既告诉我们哪些滑移系开动,又指导我们分析开动滑移系转动的方向和为什么这个取向随变形的进行,取向却是稳定而不改变的。
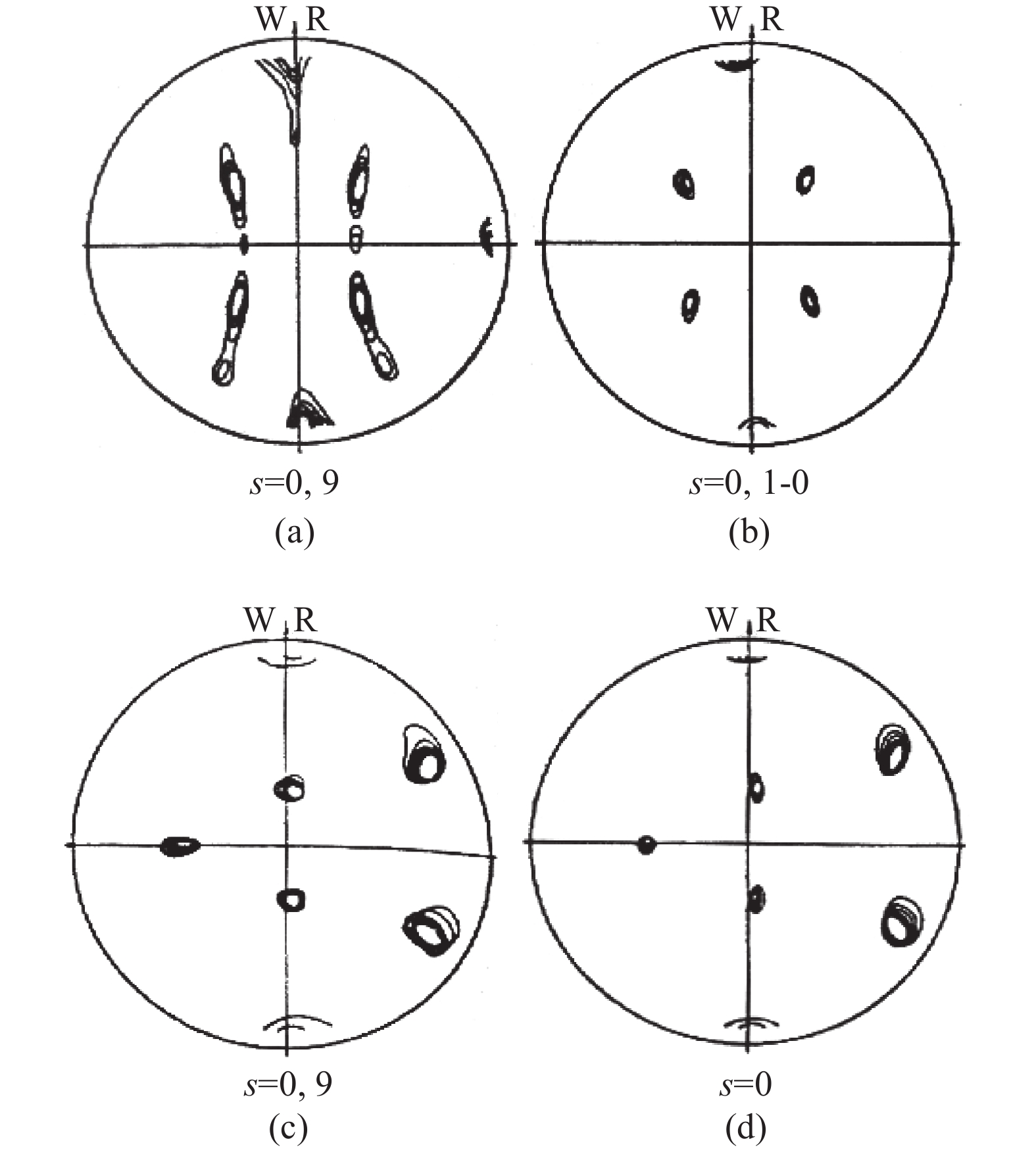
图17为用极图表示不同取向BCC结构Fe-3Si单晶轧制时沿板厚度方向形变均匀性的差异。冷轧时不同单晶的取向变化显示不同的取向稳定性;旋转立方取向(100)[011]晶体轧制后,板材的表层出现绕横向轴转动,而板中心层取向不变,见图17(a)和(b)。(112)[
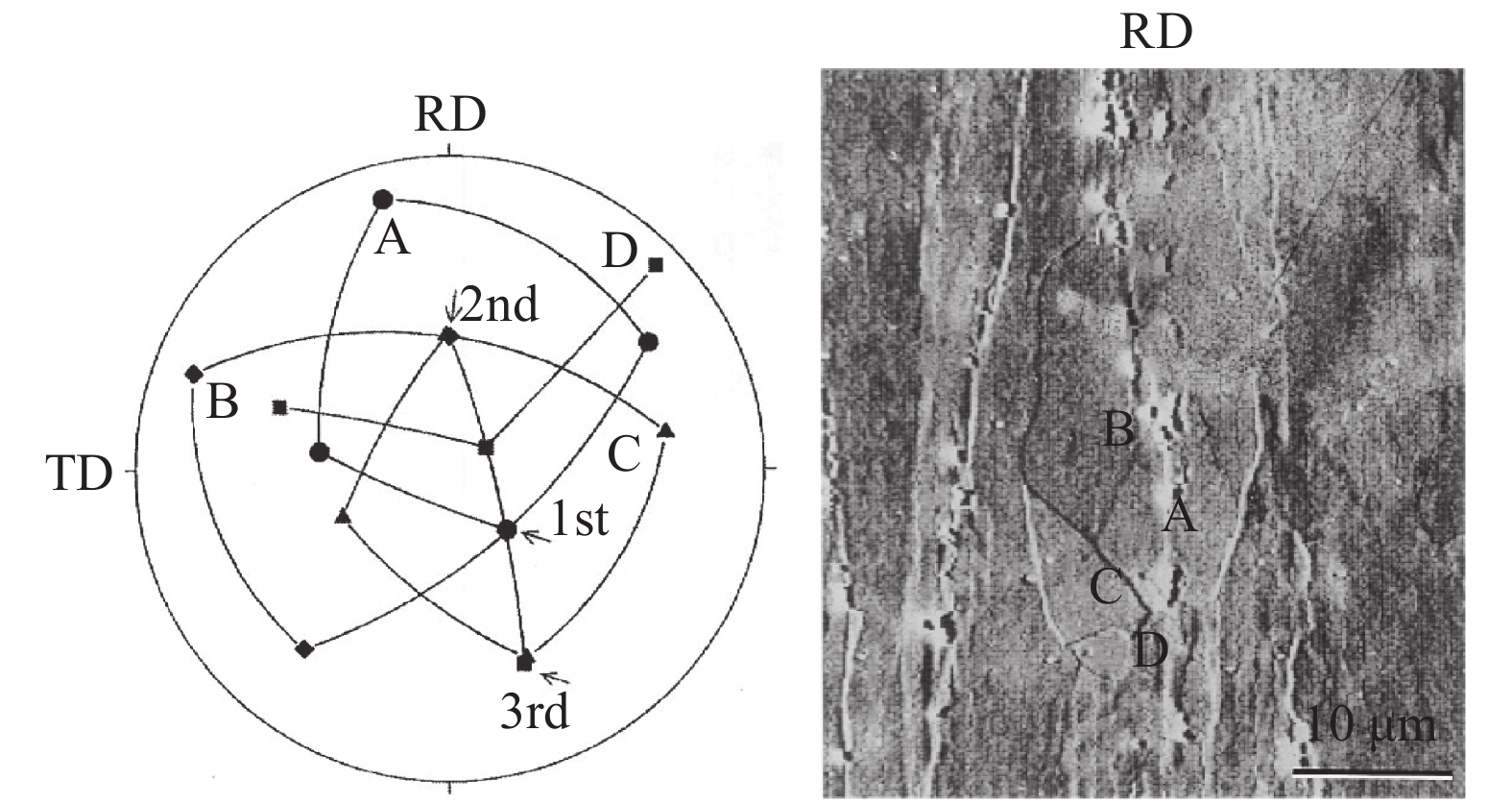
图18为在极图上表示高层错能的Al-1.3Mn合金轧制再结晶初期后出现的3阶孪晶关系,是作者1994年在德国亚琛工业大学攻读博士学位阶段用EBSD技术检测到的,测定时间1 min左右,测定时自然不知道各晶粒之间是什么关系,但一旦用{111}极图显示出来,便能确定其是由A→B→C,B→D的孪生关系;该结果发表在文章[10]中。
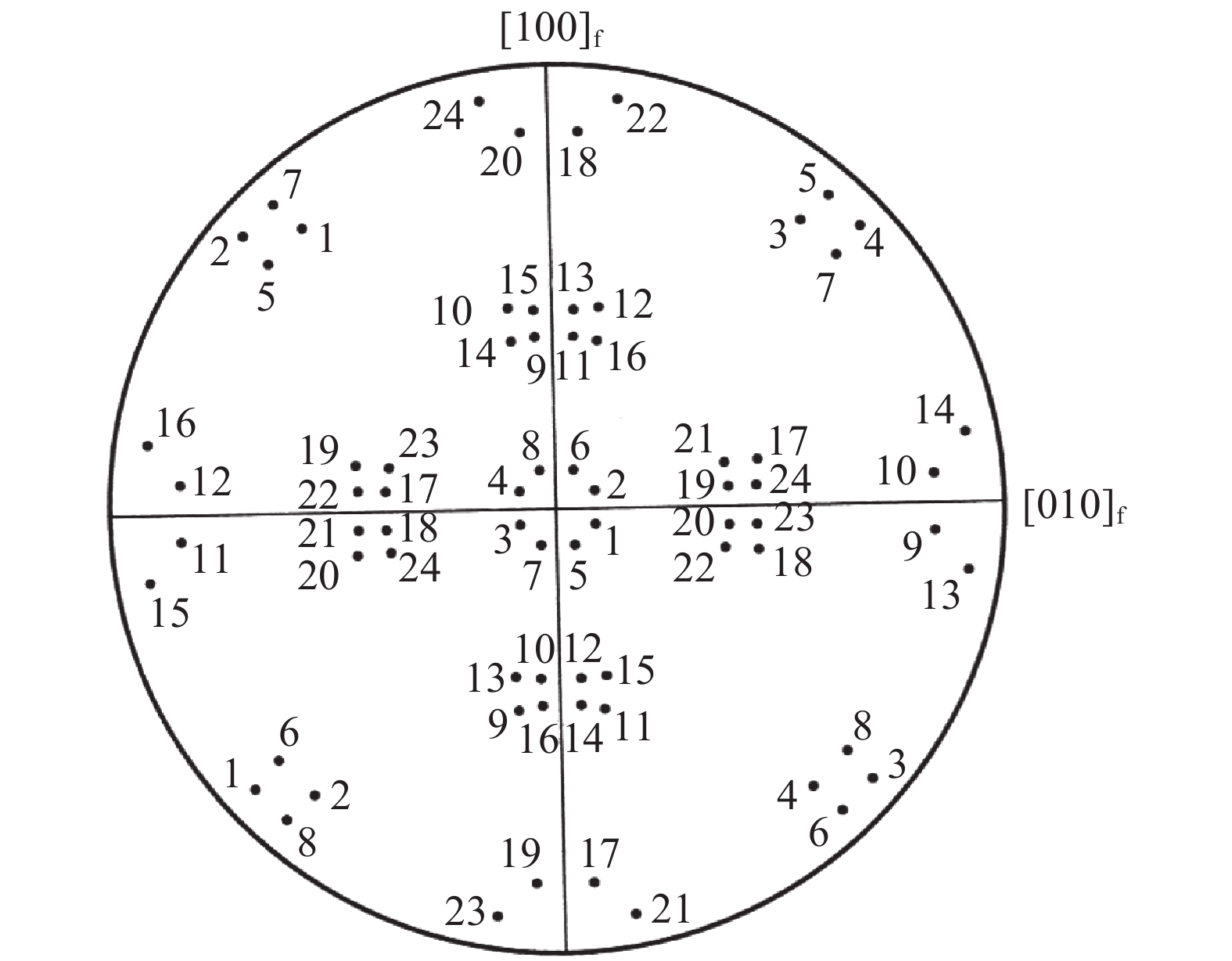
图19为用{100}极图的方式表示面心-体心结构晶体按K-S取向关系相变时各变体的位置、数目及分布。一个面心立方结构的{100}<001>立方取向晶粒按K-S关系可转变为24个体心立方结构的马氏体变体。每个取向有3个{100}投影点,24个取向共72个点。分属于3种类型取向,每组8个取向。第一组近似为45°旋转立方取向{100}<011>(图中1-8#),第二组近似为反高斯取向
多晶体的择优取向问题几乎总是借助于极射赤面投影来分析解决的。此外单晶体和某些多晶体中的—些有方向性的力学或物理性质,如弹性模量、屈服点和导电率等,可以在极射赤面投影上用图解法表示。
4. 结束语
极射投影法是直观的三维方向关系表达法,极射投影图使其变为二维纸面上的关系;涉及的领域从天体学、地理学、航行测绘、地质学、晶体学、材料科学、数学等;在尺度上从纳米尺度的晶体单胞到工件、微电子器件到矿物岩石、山体滑坡到地震灾害、地球太阳到宇宙。在时间上从古至今,在地域上遍及各大洲,离我们那么远又那么近,只要有心,那就是那么有趣。人既要在某一方面深入下去,也要有对多领域的了解,提高触类旁通的能力。
来源--金属世界





 下载:
下载: