分享：TC17钛合金热变形行为及本构模型

温飞娟1,温奇飞2,龙 樟3,宋 檬3,曹立清1

 (1.西南石油大学新能源与材料学院,南充637001;2.南充市特种设备监督检验所,南充637000; 3.西南石油大学机电工程学院,南充637001) 

摘 要:对TC17钛合金进行不同温度(600~950℃)和不同应变速率(0.001~10s-1)的热压 缩试验,研究了TC17钛合金的热变形行为,建立了 TC17钛合金多元线性回归本构模型,并进行 了试验验证。结果表明:TC17钛合金的流变应力随变形温度的升高而减小,随应变速率的增大而 增大;在低温段(600~850 ℃)变形时,真应力-真应变曲线整体上呈应变软化特征,在高温段 (850~950℃)变形时,则呈稳态流动特征,流变应力软化现象不明显;由 TC17钛合金多元线性回 归本构模型得到的流变应力的计算值与试验值较为接近,模型具有较高的预测精度。

 关键词:TC17钛合金;热变形行为;Arrhenius方程;本构模型 中图分类号:TG146 文献标志码:A 文章编号:1000-3738(2023)08-0086-07

0 引 言

 钛合金由于密度低,强韧性好,常用于航天发动 机和飞机壳体的轻量化设计制造[1-5]。TC17钛合 金是一种富β相的α-β型钛合金,由于具有高强度、 高韧性以及高淬透性,因此又被称为“三高钛合 金”[6-8]。但TC17钛合金的热加工工艺复杂,经过 锻造后显微组织均匀性差,严重影响着其力学性 能[9]。材料的热变形行为是制定其热加工工艺的基 础,热变形后材料的组织和性能取决于热变形过程 中加工硬化和动态软化的相互作用,而硬化和软化 过程受多种因素的影响,其中变形温度和应变量的 影响最大[10-11]。此外,研究[12-13]表明,TC17钛合金 在热变形时的流变应力与应变速率和变形温度之间具有复杂关系。因此,了解 TC17钛合金在热变形 时流变应力与应变速率、变形温度及应变量的关系 对改善其热加工工艺有着重要指导意义。 使用有限元方法对TC17钛合金加工过程进行 模拟,获得其热加工过程中的温度、应变和应力分布 信息,可以更深层次地研究其加工工艺,优化工艺参 数[14],但这依赖于可靠的材料本构模型[15-16]。目前 常用的本构模型包括Johnson-Cook(J-C)模型[17]、 Zerilli-Armstrong(Z-A)模型及双曲正弦模型[18]。 杨晓康等[19]对J-C模型进行修正,修正的模型能较 好地描述TC17钛合金的高温流变行为。目前国内 对TC17钛合金本构关系的研究还很少,而关于双 曲正弦模型对于 TC17钛合金的适用性研究则更 少。因此,作者对 TC17钛合金的热压缩变形行为 进行研究,构建了精度满足要求的本构模型,并对本 构模型进行了验证,拟为 TC17钛合金热加工过程 的有限元模拟提供理论参考。 

1 试样制备与试验方法 

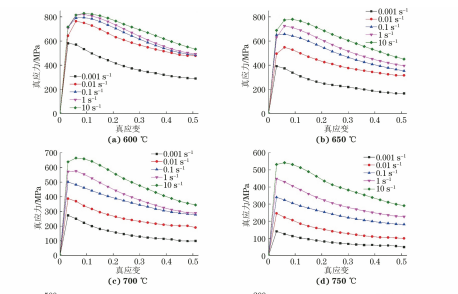
试验材料为经过单相区等温锻造+固溶+时效 处理的TC17钛合金棒,其原始显微组织为α+β网 篮组织,如图1所示。将钛合金棒机加工成尺寸为 ?8mm×12mm的圆柱形试样。在 Thermecmaster-Z型热模拟试验机上对试 样进行等温恒应变速率压缩试验,为防止热压缩过 程中试样出现鼓肚,在试样两端垫云母片以降低试 样与压头之间的摩擦力。设置应变速率分别为 0.001,0.01,0.1,1,10s-1,变形温度分别为600, 650,700,750,800,850,900,950 ℃,升温速率为 10℃·s-1,达到变形温度后保温5min进行压缩, 最大高度压下率为40%,对应的真应变约为0.51。 试验过程中用安装在试样侧面中部的热电偶实时测 定试样温度,将试样温度控制在变形温度的±1℃ 范围内波动。压缩后的试样立即在氩气中冷却至 室温。

 2 试验结果与讨论

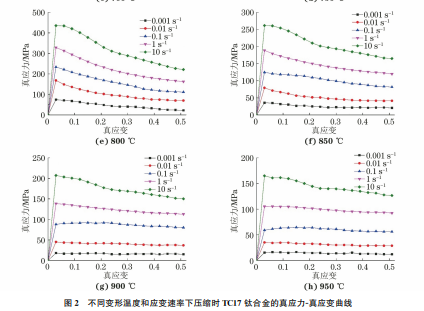
 由图2可见,不同变形温度下压缩时 TC17钛 合金的真应力-真应变曲线变化趋势基本相同,整体 可划分为3个阶段:在变形初期,位错密度随应变的 增加而增大,产生加工硬化,流变应力随着应变的增 大迅速增大;随后,随着应变量增加,位错通过攀移 或交滑移的方式进行运动,并在热能和外加应力的 综合作用下发生合并与重组,使材料发生动态软化, 并逐渐成为主要控制机制,流变应力增大趋势减小, 应力在达到峰值后,开始缓慢下降[20];在变形末期, 加工硬化与动态软化达到动态平衡,曲线趋于平 缓[21],并且温度越高,这种现象越发明显。 在相同的应变速率下,流变应力随变形温度的 升高而降低。这是因为一方面随着变形温度的升 高,材料的活化能增大,原子获得的能量增多,平均 动能增大,材料更容易发生滑移;另一方面,高温条 件下更容易发生动态回复和动态再结晶,位错密度 的降低弱化了塑性变形引起的加工硬化,进而降低 了材 料 的 流 变 应 力。当 变 形 温 度 较 低 (600~ 850℃)时,流变应力对变形温度的变化十分敏感, 当应变速率为0.1s-1 时,变形温度每升高50 ℃, 峰值 应 力 分 别 降 低 136.8,156.8,160.9,106.4, 105.1MPa;当变形温度较高(850~950℃)时,流变 应力对温度的敏感性下降,变形温度每升高50℃,峰 值应力仅分别降低32.5,27.6MPa。TC17钛合金在 低温段(600~850℃)变形时,真应力-真应变曲线整 体上呈应变软化特征,而在高温段(850~950℃)变 形时,真应力-真应变曲线整体呈稳态流动特征。 在相同的变形温度下,流变应力随应变速率的 增大而增大。当应变速率增加时,位错数量增多导 致临界剪切应力升高,同时由于塑性变形时间缩短, 动态软化作用减弱,使得硬化过程更为明显,流变应 力增大;此外,由于没有充足的时间通过位错运动及 相邻晶粒协调变形使应力松弛,合金内部存在较大 的应力集中,同样会导致流变应力增大。流变应力 对应变速率的敏感程度随温度的变化明显不同, 800℃是流变应力对应变速率敏感程度的临界温 度:当变形温度低于800℃时,流变应力对应变速率 的敏感程度随变形温度的升高而增大;当变形温度 高于800℃时,流变应力对应变速率的敏感程度随 变形温度的升高而降低。

 3.1 Arrhenius方程

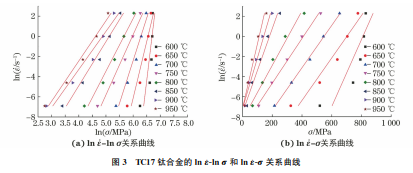
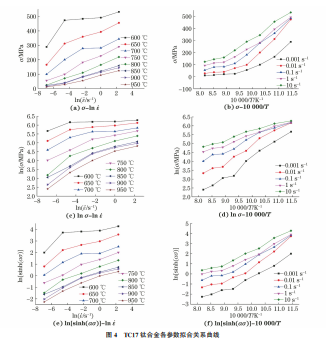
 一般来说,建立本构关系的方法有两种:一种是预 先假定材料流动行为的变形机理,然后根据材料的相 关常数确定本构关系;另一种是在试验应变速率范围 和温度内测定流变应力,对试验结果进行数理统计以 确定本构关系。第一种方法具有一定的局限性,依赖 于材料本身的参数变化,难以精确描述变形机理。第 二种方法不需要考虑复杂的材料内部参数,且在相当 宽的温度范围内有效,因而得到了广泛的应用[22-23]。 许多学者对金属变形的动态响应方程提出了不 同的本构模型,其中比较著名的是由Sellar等提出 的 Arrhenius方程[24],其表达式为 ε ·exp Q RT =Asinh(ασ)n (1) 式中:ε · 为应变速率;σ为流变应力;Q 为热变形激活 能;R 为气体常数;T 为变形温度;A,α,n为材料参数。在低应力区,即ασ<0.8时,Arrhenius方程可 表示为 ε ·exp Q RT =A1σ n1 (2) 在高应力区,即ασ>1.2时,Arrhenius方程可 表示为 ε ·exp Q RT =A2exp(n2σ) (3) 式中:A1,A2,n1,n2 均为材料参数。 分别对式(1)、式(2)、式(3)两边取对数可得: ln[sinh(ασ)]= 1 n lnε ·+ Q nRT - lnA n (4) lnσ= 1 n1 lnε ·+ Q n1RT - lnA1 n1 (5) σ= 1 n2 lnε ·+ Q n2RT - lnA2 n2 (6) 式(4)、式(5)、式(6)的统一形式如下: f(σ)=B+Clnε ·+ D T (7) 式中:f(σ)分别对应于式(4)、式(5)和式(6)中的 ln[sinh(ασ)]、lnσ和σ;B,C,D 分别对应各方程中 相应的系数项。 Arrhenius方程中,双曲正弦函数形式具有较广的 适用性。在验证Arrhenius方程的适用性时,需要先确 定双曲正弦函数形式中的α值。由文献[25-27]可知: α= n2 n1 (8) n1 = ∂lnε · ∂lnσ (9) n2 = ∂lnε · ∂σ (10) 采用TC17钛合金热压缩试验数据,绘制lnε ·- lnσ和lnε ·-σ曲线并进行最小二乘法线性回归,结 果如图3所示。lnε ·-lnσ和lnε ·-σ曲线的斜率分别 为n1 和n2 值,计算得到n1=3.815,n2=0.054,因 此α=0.011。 3.2 适用性检验 由式(7)可知,函数f(σ)与变量lnε · 和T-1 成 双线性关系是使用 Arrhenius方程的前提条件。绘 制 TC17钛合金的σ-lnε ·、σ-10000/T、lnσ-lnε ·、 lnσ-10000/T、ln[sinh(ασ)]-lnε ·、ln[sinh(ασ)]- 10000/T 关系曲线,由图4可见,f(σ)与lnε · 和 10000/T 之间无双线性关系,这说明3种形式的 Arrhenius方程均不适用于TC17钛合金。 

3.3 本构关系的建立 

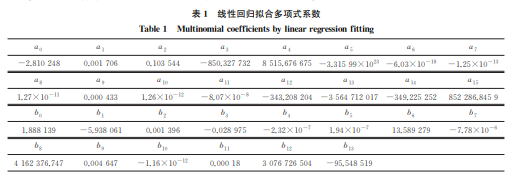
由于3种形式的 Arrhenius方程均不适用于 TC17钛合金,因此在考虑应变速率、应变和变形温 度的前提下,提出基于逐步回归法构建的多元线性 回归本 构 模 型[28]。将 整 个 变 形 温 度 范 围 分 成 (600~850℃)和(850~950 ℃)两个温度段,分别 构建本构模型,如下: lnσ=a0 +a1ε+a2 ε ·5 T +a4 1 T +a5 1 T8 +a6 T·ε 6 +a7 T·ε 3 +a8T3· lnε 2 +a9T·lnε ·+ a10 T·lnε · 3 +a11 lnε ··lnε 5 +a12 lnε T +a13 lnε T 4 +a14 lnε · T +a15 lnε · T 3 (600~850℃)(11) lnσ=b0 +b1ε+b2 ε ·5 T +b3 lnε 2 +b4 lnε 7 +b5 ε·T ε · +b6 lnε·lnε · T +b7ε ··T·lnε+ b8 1 T2 +b9T·ε+b10T3· lnε 4 +b11T·lnε+b12 lnε T 4 +b13 lnε · T (850~950℃) (12)

3.4 本构关系的误差检验

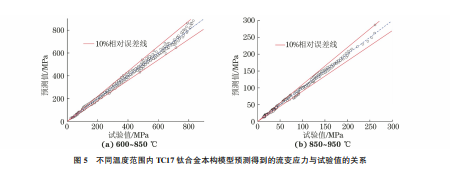
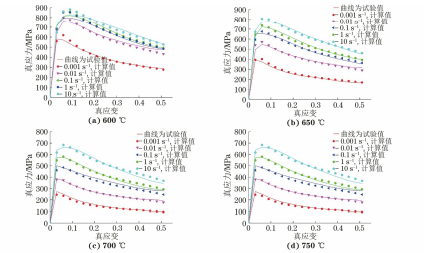
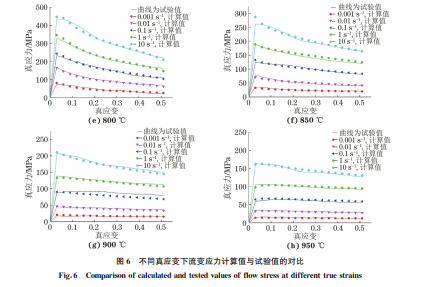
 由图5可见,在600~850℃和850~950℃两个 温度段内,相对误差在±10%以内的数据点分别占 全部数据点的95.53%和91.76%,同时求得式(11) 和式(12)的复相关系数R 均较高,分别为0.994和 0.998,说明预测数据与实际数据误差较小。 由图6可见,由本构模型得到的流变应力计算 值 与试验值比较接近,说明所建立的TC17钛合金的本构模型对流变应力具有较高的计算精度。 

4 结 论

 (1)TC17钛合金流变应力对变形温度和应变 速率均具有较高的敏感性,流变应力随变形温度的 升高而减小,随应变速率的增大而增大。 (2)在低温段(600~850 ℃)变形时,TC17钛 合金的真应力-真应变曲线整体上呈应变软化特征; 在高温段(850~950 ℃)变形时,真应力-真应变曲 线整体呈稳态流动特征,流变应力软化现象不明显。 (3)建立了 TC17钛合金在600~850 ℃ 和 850~950℃两个温度段的多元线性回归本构模型 由本构模型得到的流变应力的计算值与试验值的误 差较小,具有较高的预测精度.

来源：材料与测试网