分享：F690超高强钢的腐蚀疲劳裂纹扩展行为及其有限元模拟

马颖涵1,张 振1,2,郭孟雨1,赵 伟1,2,张才毅3,胡正飞4,高 珊3 

(1.南京工程学院材料科学与工程学院,南京211167;2.江苏省先进结构材料与应用技术重点实验室, 南京211167;3.宝山钢铁股份有限公司研究院,上海 201900;4.同济大学材料科学与工程学院,上海 201804) 

摘 要:采用直流电压降法测试了 F690超高强钢在模拟海水中的疲劳裂纹扩展速率,研究了 应力比(0.1,0.2,0.3)和加载频率(0.15,0.30,0.60Hz)对疲劳裂纹扩展行为的影响;采用基于能量 释放率 Paris法则的扩展有限元方法对腐蚀疲劳过程进行了模拟,并与试验结果进行对比。结果 表明:F690钢在模拟海水中的腐蚀疲劳裂纹扩展速率随着应力比或频率的增大而减小;腐蚀疲劳 断裂形式为穿晶断裂,且随着频率增加,二次裂纹的宽度变小;模拟得到 F690钢的腐蚀疲劳裂纹 扩展长度与试验结果相吻合,相对误差小于0.6%,说明采用该扩展有限元方法可有效模拟和预测 F690钢的腐蚀疲劳裂纹扩展行为。

 关键词:F690钢;腐蚀疲劳;裂纹扩展速率;扩展有限元 中图分类号:TG172.5 文献标志码:A 文章编号:1000-3738(2021)04-0065-07

0 引 言 

随着人类社会的快速进步与发展,石油、天然气 等不可再生资源的需求量与日俱增,但陆地资源是 有限的,人们终将面对陆地资源枯竭的问题,因此蕴 藏丰富资源且尚未被开发的海洋吸引了人们的关 65 马颖涵,等:F690超高强钢的腐蚀疲劳裂纹扩展行为及其有限元模拟 注。截至2015年,海洋石油的开采量已占石油总产 量的39% [1]。海洋勘探设备在海洋资源的开采中 起到了重要的作用,因此海洋工程用钢应具有优异 的综合性能。目前,屈服强度达到690 MPa的海洋 工程用超高强钢逐渐投入使用[2-3],这也为海洋资源 向深海和极地的开发提供了条件。 在复杂的海洋环境中,海洋工程用钢在腐蚀环 境和疲劳载荷共同作用下会产生裂纹扩展损伤,从 而对设备的安全服役产生不利影响。因此,研究海 洋工程用钢的腐蚀疲劳裂纹扩展行为十分重要。目 前,关于海洋工程用材料的腐蚀疲劳行为已有一些 研究。张振等[4]和王琪等[5]研究发现,F690钢在模 拟海水中的静态腐蚀形貌整体上呈现均匀腐蚀特 征,而在空气中的疲劳裂纹以条带机制扩展,断裂方 式为穿晶断裂。MA 等[6-7]研究发现:E690钢在模 拟海水中具有一定的应力腐蚀开裂(SCC)敏感性, 且在高阴极电位下具有较高的氢脆敏感性;在大角 度晶界和马氏体-奥氏体(M-A)与相邻铁素体之间 的微电偶效应下,原奥氏体晶界处容易产生晶间微 裂纹。ZHAO 等[8-9]研究发现,在模拟海水中,E690 钢腐蚀疲劳裂纹的萌生和扩展机制随峰值应力水平 的升高而改变,只有在峰值应力接近或高于屈服点 时,环境中的氢才会显著影响材料的疲劳寿命。王恒 等[10]研究发现,随着应力比增大,E690高强钢的腐蚀 疲劳裂纹扩展速率增大,裂纹扩展门槛值降低。 目前,国内外有关 F690 超高强钢在腐蚀环境 中的腐蚀疲劳裂纹扩展行为的研究报道较少,尤其 是应力比、频率、应力幅对F690超高强钢腐蚀疲劳裂 纹扩展行为影响的研究报道更少。因此,作者以通 过船级社认证的最高等级国产高强韧船板 F690钢 为研究对象,采用直流电压降方法测该钢在模拟海 水中的疲劳裂纹扩展速率,研究应力比和加载频率 对疲劳裂纹扩展行为的影响,并观察疲劳断口形貌; 采用基于能量释放率 Paris法则的扩展有限元方法 对腐蚀疲劳过程进行模拟,并与试验结果进行对比。 

1 试样制备与试验方法 

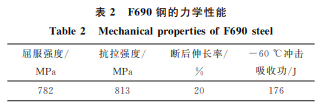
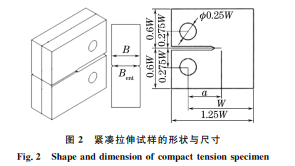
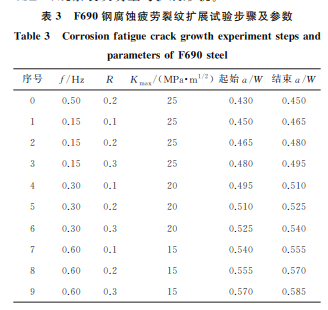
试验材 料 为 国 内 某 钢 厂 已 实 现 量 产 的 F690 厚钢板,其 热 处 理 工 艺:895 ℃ ×170 min水 淬 + 650 ℃×240 min回 火 处 理,出 炉 后 水 冷 至 室 温。 F690钢的显微组织如图1所示,组织为板条贝氏 体。化学 成 分 和 力 学 性 能 分 别 如 表 1 和 表 2 所 示。腐蚀疲劳裂纹扩展试样为紧凑拉伸(CT)试样, 按照 ASTM E647-12,在试验钢上加工出如图2所 示的 CT 试样,CT 试样的宽度 W 为25.4 mm,厚 度B 为12mm。为了保证裂纹尽量沿垂直于加载 的方向扩展,同时避免产生裂纹分支,在试样两侧 面开深度Bent 为5%B 的侧槽,有效厚度 Beff 定义 为(B·Bent)1/2。 图1 F690钢的原始显微组织 Fig.1 OriginalmicrostructureofF690steel 表1 F690钢的化学成分 质量分数 Table1 ChemicalcompositionofF690steel massfraction % C Mn P S Si Cr Mo Cu Ni Nb Fe 0.07 1.03 0.008 0.002 0.21 0.60 0.47 0.6 1.68 0.042 余 表2 F690钢的力学性能 Table2 MechanicalpropertiesofF690steel 屈服强度/ MPa 抗拉强度/ MPa 断后伸长率/ % -60 ℃冲击 吸收功/J 782 813 20 176 按 照 GB/T 6398-2000,采 用 直 流 电 压 降 (DCPD)方法[11-12]在电液伺服应力腐蚀试验机上进 行腐蚀疲劳裂纹扩展试验,腐蚀环境为模拟海水环 境(质量分数3.5%NaCl溶液),温度为室温(20 ℃), 加载波形 为 正 弦 波,采 用 恒 定 最 大 应 力 强 度 因 子 图2 紧凑拉伸试样的形状与尺寸 Fig.2 Shapeanddimensionofcompacttensionspecimen Kmax 控制总应力来施加载荷;预制疲劳裂纹通过最 大加载载荷(Kmax=25 MPa·m 1/2)来实现,预制疲 66 马颖涵,等:F690超高强钢的腐蚀疲劳裂纹扩展行为及其有限元模拟 劳裂纹长度为0.5mm,裂纹扩展长度a 的起始值为 11mm;试验过程中的应力比R 为0.1,0.2,0.3,加 载频 率 f 为 0.15,0.30,0.60 Hz,Kmax 为 15,20, 25MPa·m 1/2,试验步骤如表3所示,序号0指初始 预制疲劳裂纹,然后依次进行9组不同频率和应力 比的裂纹扩展试验。随着试验的进行,加载载荷逐 渐降低,以保证裂纹尖端所受应力不变。通过试验 仪器直接在线监测和记录裂纹扩展长度,并在试验 结束后 采 用 ZEISS MERLIN 型 扫 描 电 子 显 微 镜 (SEM)观察裂纹萌生与扩展形貌。 

 2 试验结果与讨论

 2.1 腐蚀疲劳裂纹扩展速率

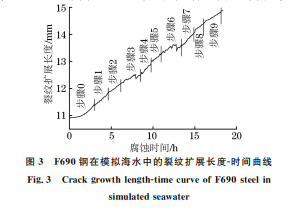
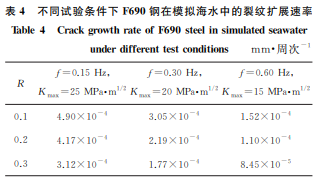
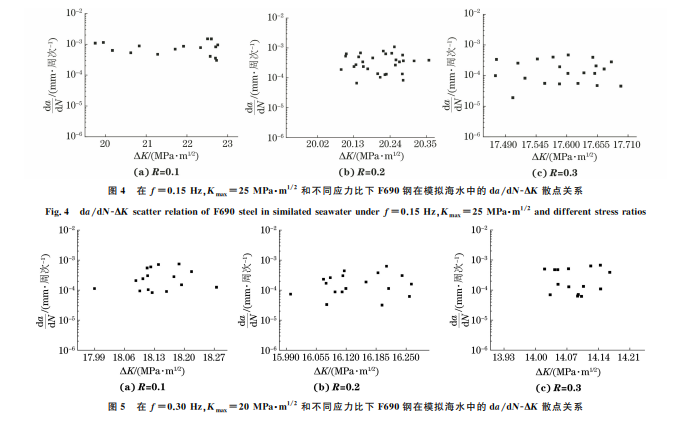
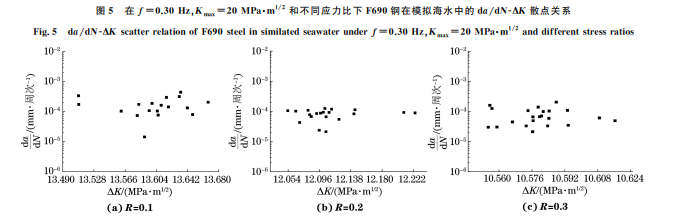
 图3 F690钢在模拟海水中的裂纹扩展长度-时间曲线 Fig.3 Crackgrowthlength-timecurveofF690steelin simulatedseawater 由图3可以看出:裂纹在形成阶段的扩展速率 较为缓慢,当裂纹形成一段时间后其扩展速率达到 稳定。将裂纹扩展长度-时间(t)曲线波动范围较大 的部分舍去后,根据疲劳裂纹扩展速率da/dt,再由 频率与时间的关系(f=1/t),即可得到裂纹扩展速 率da/dN。由表4可以看出,随着应力比或频率的 增加,腐蚀疲劳裂纹扩展速率降低。因此,可以通过 改变应力比和频率来减小 F690钢在海水中的疲劳 裂纹扩展速率,从而提高其使用寿命[13]。在腐蚀环 境中裂纹扩展速率受腐蚀介质的影响较大,频率越 低,裂纹尖端与腐蚀介质接触的时间越长,腐蚀作用 越明显,因此裂纹扩展速率越大。 表4 不同试验条件下F690钢在模拟海水中的裂纹扩展速率 Table4 CrackgrowthrateofF690steelinsimulatedseawater underdifferenttestconditions mm·周次-1 R f=0.15Hz, Kmax=25MPa·m 1/2 f=0.30Hz, Kmax=20MPa·m 1/2 f=0.60Hz, Kmax=15MPa·m 1/2 0.1 4.90×10 -4 3.05×10 -4 1.52×10 -4 0.2 4.17×10 -4 2.19×10 -4 1.10×10 -4 0.3 3.12×10 -4 1.77×10 -4 8.45×10 -5 由应力强度因子范围 ΔK 的计算公式[14]: ΔK = ΔP 1000B W (2+α) (1-α)3/2 × (0.886+4.64α-13.32α 2 +14.72α 3 -5.6α 4) (1) α= a W (2) 式中:ΔP 为施加载荷的范围,kN。 不同试验参数下 F690钢在模拟海水中的裂纹 扩展速率与应力强度因子范围的散点关系如图4~ 图6所示。由图4~图6可以看出,应力比越大、频 率越高,da/dN 曲线越向低 ΔK 方向移动,这是由 于应力比和频率可以显著影响腐蚀疲劳裂纹扩展门 槛值。应力比越大、频率越高,由近门槛值区进入裂 纹稳定扩展区域的应力强度因子范围越小。 裂纹扩展速率与应力强度因子范围的关系可用 Paris公式进行描述,其表达式为 da dN =C(ΔK)m (3) 式中:C 和m 均为材料常数,受温度、介质、应力比、 加载频率等因素的影响。 对式(3)两边取对数,得: lg da dN =mlg(ΔK)+lgC (4) 基于式(4)对腐蚀疲劳试验数据进行拟合,得到 材料常数C 和m 如表5所示。由表5可以看出:在 较低加载频率(0.15 Hz)下,随着应力比增大,m 增 大,C 减小;在较高频率(0.30,0.60 Hz)下,二者随 应力比的变化规律并不显著。 67 马颖涵,等:F690超高强钢的腐蚀疲劳裂纹扩展行为及其有限元模拟 图4 在f=0.15Hz,Kmax=25MPa·m 1/2 和不同应力比下F690钢在模拟海水中的da/dN-ΔK 散点关系 Fig.4 da/dN-ΔKscatterrelationofF690steelinsimilatedseawaterunderf=0.15Hz,Kmax=25MPa·m 1/2anddifferentstressratios 图5 在f=0.30Hz,Kmax=20MPa·m 1/2 和不同应力比下F690钢在模拟海水中的da/dN-ΔK 散点关系 Fig.5 da/dN-ΔKscatterrelationofF690steelinsimilatedseawaterunderf=0.30Hz,Kmax=20MPa·m 1/2anddifferentstressratios 图6 在f=0.60Hz,Kmax=15MPa·m 1/2 和不同应力比下F690钢在模拟海水中的da/dN-ΔK 散点关系 Fig.6 da/dN-ΔKscatterrelationofF690steelinsimilatedseawaterunderf=0.60Hz,Kmax=15MPa·m 1/2anddifferentstressratios 表5 拟合得到不同试验条件下的材料常数 Table5 Materialconstantsunderdifferenttestconditions obtainedbyfitting R f=0.15Hz, Kmax=25MPa·m 1/2 f=0.30Hz, Kmax=20MPa·m 1/2 f=0.60Hz, Kmax=15MPa 1/2 C m C m C m 0.1 8.54×10 -7 1.60 6.38×10 -12 5.60 4.76×10 -13 7.27 0.2 2.64×10 -8 2.47 2.36×10 -13 6.87 5.00×10 -12 6.41 0.3 4.07×10 -9 2.96 8.62×10

 -12 5.97 4.20×10 -13 7.77

 2.2 腐蚀疲劳断口形貌

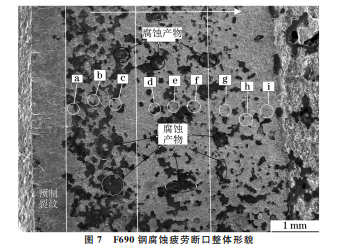
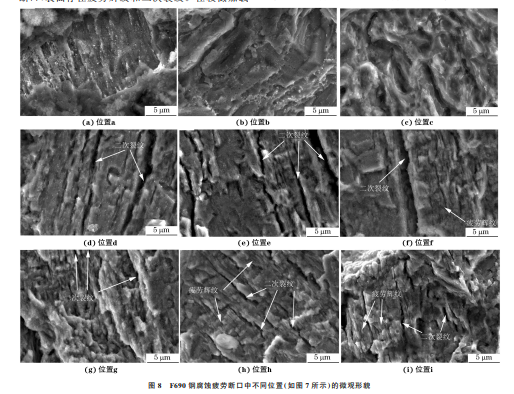
 图7为 F690钢腐蚀疲劳断口整体形貌,图中 箭头表示裂纹扩展方向。由图7可以看出,断口表 面存在较多的腐蚀产物,且由于裂纹扩展初期的断 图7 F690钢腐蚀疲劳断口整体形貌 Fig.7 OverallmorphologyofcorrosionfatiguefractureofF690steel 68 马颖涵,等:F690超高强钢的腐蚀疲劳裂纹扩展行为及其有限元模拟 口表面接触腐蚀介质的时间更长,因此该区域的腐蚀 产物更多[14]。图7中的位置a,b,c对应f=0.15Hz, Kmax=25MPa·m 1/2 的裂纹扩展区,位置d,e,f对应 f=0.30Hz,Kmax=20MPa·m 1/2 的裂纹扩展区,位 置g,h,i对应f=0.60Hz,Kmax=15 MPa·m 1/2 的 裂纹扩展区。由图8可以看出:断口性质为穿晶型 断口,表面存在疲劳辉纹和二次裂纹。在较低加载 频率(0.15Hz)下,疲劳辉纹和二次裂纹并不显著, 推测是由疲劳辉纹和二次裂纹被大量腐蚀产物覆盖 所致。当加载频率为0.30 Hz时,二次裂纹清晰可 见,且其长度和宽度均较大。但当加载频率进一步 增加至0.60Hz时,二次裂纹宽度明显变小,这是由 于频率增大加快了裂纹尖端的应变速率和闭合速 率,从而抑制了二次裂纹的萌生与扩展。 

 3 有限元模拟与试验验证 

3.1 模拟参数设置

 扩展有限元法采用不连续的加强形函数来解决 间断问题,使裂纹扩展的模拟问题更加简单,模拟精 度较相同网格下的常规有限元法更精确,计算效率 显著提高。采用扩展有限元法对 F690钢的腐蚀疲 劳试验步骤1、2、3进行模拟。疲劳裂纹的起裂和扩 展遵循 Paris公式,该定律将相对断裂能释放速率 G 与疲劳裂纹扩展速率相关联。在低周期疲劳分析 中,疲劳裂纹扩展起始准则用单元在其最大值和最 小值之间加载时的相对断裂能量释放率 ΔG 来表 示。疲劳裂纹扩展起始准则定义[15]为 f=N/(c1ΔG c2 )≥1.0 (5) 式中:c1 和c2 为材料常数;N 为疲劳循环次数。 当单元加载过程中的最大断裂能量释放率超过 门槛值,且满足以上判断准则时,裂纹尖端单元开始 发生断裂失效,此时裂纹扩展速率可由下式表示: da/dN =c3ΔG c4 (6) 式中:c3 和c4 均为材料常数。 69 马颖涵,等:F690超高强钢的腐蚀疲劳裂纹扩展行为及其有限元模拟 基于试验数据,拟合得到的材料常数以及其他 试验参数如表6所示,其中GIC 是I型裂纹的临界 能量释放率。 表6 有限元模拟用材料参数 Table6 Materialparametersforfiniteelementsimulation 弹性模量/ GPa 泊松比 c1 c2 c3 c4 GIC 323.4 0.3 0.17 -0.17 1.40688×10 -5 1.55 52

 3.2 有限元模型的建立

 在 CT 试 样 两 端 圆 孔 内 施 加 约 束 和 循 环 载 荷[16],采用 ABAQUS软件建立 CT 试样的几何模 型并对其进行网格划分,单元类型采用C3D8R轴对 称,网格精度为0.2mm,如图9所示。采用恒应力 强度因子加载,应力比分别为0.1,0.2,0.3,根据试 图9 CT试样有限元模型网格划分 Fig.9 MeshgenerationoffiniteelementmodelofCTsample 验导出的载荷与时间数据,采用三角波载荷来近似 模拟正弦波载荷,如图10所示,可知模拟载荷与试 验载荷相吻合。 

3.3 模拟结果与试验验证

 由图11可知,随着加载时间延长,预制裂纹尖端 图10 试验与模拟载荷的对比 Fig 10 Comparisonofloadingbetweentest a andsimulation b 图11 模拟得到不同加载时间下的疲劳裂纹扩展与裂纹尖端应力分布 Fig.11 Fatiguecrackgrowthandstressdistributionofcracktipatdifferentloadingtimeobtainedbysimulation 70 马颖涵,等:F690超高强钢的腐蚀疲劳裂纹扩展行为及其有限元模拟 达到起裂条件后开始扩展,扩展裂纹类型为I型裂 纹,裂纹尖端应力最大,且由中心向周围逐渐降低, 由应力分布趋势得到的塑性区形状与理论计算的大 致相同[17]。 根据不同加载时间下发生失效开裂网格单元的 长度计算得到裂纹扩展长度,并与试验结果进行对 比,由图12可以看出,采用有限元模拟得到腐蚀疲 劳裂纹扩展长度与试验结果相吻合,相对误差小于 0.6%,说明采用基于能量释放率 Paris法则的扩展 有限元方法可以有效模拟和预测 F690高强钢在海 洋环境中的疲劳裂纹扩展行为。

4 结 论

 (1)在模拟海水中,加载应力比和频率的增加 降低了 F690钢腐蚀疲劳裂纹门槛值,腐蚀疲劳裂 纹扩展速率随着应力比或频率的增大而减小。腐蚀 疲劳断裂形式为穿晶断裂,断口表面存在疲劳辉纹 和二次裂纹,且随着频率增加,二次裂纹宽度变小, 说明二次裂纹的萌生扩展受到抑制。 (2)采用有限元模拟得到 F690钢在模拟海水 中的腐蚀疲劳裂纹扩展长度与试验结果相吻合,相 对误差小于0.6%,说明采用基于能量释放率 Paris 法则的扩展有限元方法能有效模拟和预测 F690钢 的疲劳裂纹扩展行为。 

来源：材料与测试网