分享：含硼不锈钢的热变形行为

廉晓洁1,2

 (1.太原钢铁(集团)有限公司,先进不锈钢材料国家重点实验室,太原 030003; 2.山西太钢不锈钢股份有限公司技术中心,太原 030003) 

摘 要:在304不锈钢成分基础上,添加了质量分数1.96%的硼元素,采用真空感应熔炼技术制 备含硼不锈钢,对该钢进行单道次热压缩试验,研究了该钢在900~1150 ℃和应变速率0.1~ 10s -1 条件下的热变形行为;根据试验数据,基于 Arrhenius方程并结合5次多项式拟合建立该钢 的热变形本构模型,对加工硬化率-真应力曲线进行分析确定该钢发生动态再结晶的临界条件。结 果表明:在试验参数下热压缩后,含硼不锈钢的流变应力-应变曲线为典型的动态再结晶型,软化机 制以动态再结晶为主;随着变形温度的升高或应变速率的减小,试验钢的峰值应力及其对应的真应 变降低;采用所建立的热变形本构方程计算得到的真应力-真应变曲线与试验测得的相吻合,平均 相对误差绝对值为2.76%,说明该本构模型能够准确预测含硼不锈钢的热变形行为;变形温度较 高、应变速率较小时,该钢较易发生动态再结晶。 

关键词:含硼不锈钢;本构模型;动态再结晶;临界应力 中图分类号:TG111.7 文献标志码:A 文章编号:1000-3738(2021)04-0081-07

0 引 言 

含硼不锈 钢 不 仅 具 有 良 好 的 吸 收 中 子 性 能, 还具有高的 强 度 和 良 好 的 韧 性,在 废 核 燃 料 储 存 及运输 的 容 器 方 面 得 到 越 来 越 多 的 应 用[1-3]。但 硼在γ相中 的 溶 解 度 很 低,过 量 添 加 硼 元 素 会 导 致不锈钢铸坯中析出硬而脆的(Fe,Cr)2B相,导致 钢的热加工性能变差,在锻造、轧制时极易造成轧 81 廉晓洁:含硼不锈钢的热变形行为 件开裂,甚至引发断裂事故[4] ;同时硼元素的加入 使不锈钢的 凝 固 态 组 织 为 共 晶 组 织,且 随 着 硼 含 量的增加,液 相 线 下 降,共 晶 硼 化 物 数 量 增 多,在 晶界处由网状连续分布变成呈棒状、团球状分布, 从而导致不锈钢的塑韧性降低[1]。目前有关含硼 奥氏体不锈 钢 的 研 究 主 要 集 中 在 硼 含 量、热 处 理 工艺等对其显微组织和性能的影响方面[5-7],但是 对其热变形行为的研究却鲜有报道。热变形行为 的研究对于 优 化 生 产 工 艺、促 进 产 品 开 发 与 提 高 产品质量等都具有非常的意义。因此,作者在304 奥氏体不锈 钢 的 成 分 基 础 上,添 加 了 质 量 分 数 为 1.96%的硼元素,采用真空感应熔炼技术制备含硼 不锈钢;通过 单 道 次 热 压 缩 试 验 获 得 该 钢 的 真 应 力-真应变曲线,基于试验数据建立该钢的热变形 本构模型,获得动态再结晶的临界条件,研究含硼 不锈钢的热 变 形 行 为,为 含 硼 不 锈 钢 的 热 加 工 工 艺制定提供理论依据。

 1 试样制备与试验方法 

在304奥氏体不锈钢成分基础上加入一定量的 硼铁合金,采用50kg真空感应熔炼炉进行熔炼,得 到含硼不锈钢铸坯,测得其化学成分(质量分数/%) 为 0.039C,1.02Mn,17.79Cr,1.66Ti,12.03Ni, 1.96B,余 Fe。 用线切割方法在铸 坯 上 截 取 尺 寸 为?10 mm ×15mm 的试样,在 Gleeble3800型热模拟试验机 上进行单道次热压缩试验,即以20 ℃·s -1的速率 将试样加热到1050 ℃保温150s,再以25 ℃·s -1 的速率加热或冷却至变形温度保温30s,然后分别 在0.1,1,10s -1 应变速率下进行压缩变形。试验 钢在变形温度1150 ℃、应变速率0.01s -1、变 形 量50%和变形温度1200 ℃、应变速率0.01s -1、 变形量30%条件下热压缩后的宏观形貌如图1所 示,可以看 出 在 变 形 量 较 大(50%)或 者 变 形 温 度 较高(1200 ℃)条 件 下,试 样 均 出 现 了 严 重 的 开 裂,且在1200 ℃热压缩后试样已出现熔化现象, 这也验证了文献[3]和文献[4]的结果,即当硼 质 量分数大于0.5%时,将试验钢加热至1200 ℃时 其热延性为零。因此,试验钢的热变形温度不应高 于1150 ℃,设置为 900,950,1000,1050,1100, 1150 ℃,变形量(工程应变)设为 30%(真应变为 0.3567)。试验结束后采用喷水方式将试样冷却到 室温。采用 EVO18型扫描电子显微镜(SEM)观察 微观形貌。 

2 试验结果与结论 

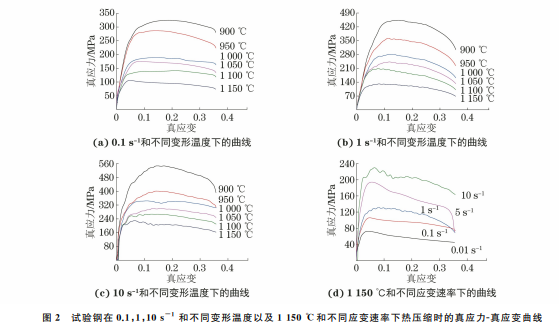
由图2可知,不同条件下热压缩后试验钢的流 变应力曲线均可分为3个阶段。当应变量较小时, 随着热压缩变形的进行,应力随着应变量的增加而 迅速增加到峰值,流变曲线呈现明显的加工硬化特 征。这是因为在热压缩过程中晶格畸变使得试验钢 组织中产生了大量的位错并形成缠结,加工硬化作 用远远大于由原子扩散和位错湮灭而引起的软化作 用[8]。随着变形的进行,再结晶的驱动力不断增大, 动态再结晶软化速率加快,在流变曲线上表现为真 应力趋于稳定值,这表明此时加工硬化作用与再结 晶软化作用处于动态平衡状态,试验钢发生了动态 再结晶[9]。当变形量继续增加时,流变曲线呈下降 趋势,这说明动态软化效应已超过了加工硬化作用。 当应变速率达到10s -1 时,900 ℃下的真应力急剧 增大至峰值,这是由低变形温度和大变形速率下位 错大量增殖所致。在相同应变速率下,随着变形温 度的升高,试验钢的峰值应力及其对应的真应变降 低,这是由于随着温度的升高,原子发生扩散和位错 发生攀移的驱动力增大,动态软化速率加快[8]。当 变形温度一定(1150 ℃)时,随着应变速率的减小, 峰值应力及其对应的真应变降低,这是由变形速率 越低,动态再结晶越容易发生所致。综上可知,在试 验条件下随着变形量的增加,真应力先迅速上升,达 82 廉晓洁:含硼不锈钢的热变形行为 图2 试验钢在0.1,1,10s -1 和不同变形温度以及1150 ℃和不同应变速率下热压缩时的真应力-真应变曲线 Fig 2 Truestress-truestraincurvesofteststeelduringhotcompressionat0 1 1 10s -1anddifferentdeformationtemperatures a-c and 1150 ℃ anddifferentstrainrates d 到峰值应力后下降,流变应力曲线呈典型的动态再 结晶型,软化机制以动态再结晶为主。

3 热变形本构方程的建立与验证

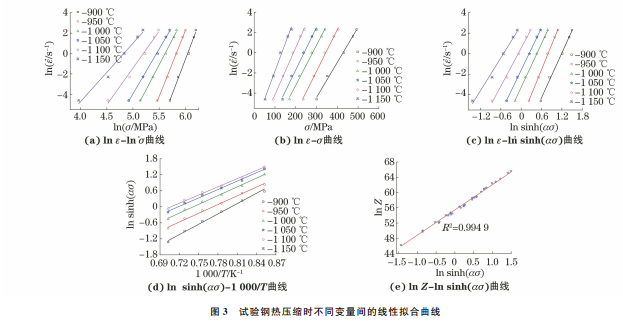
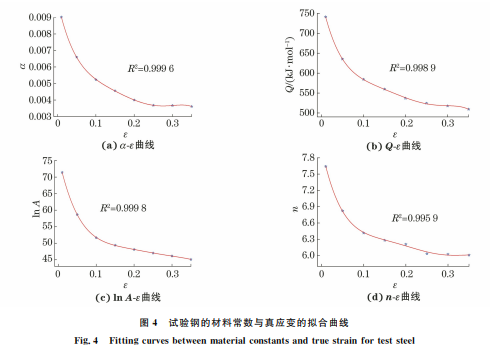
 3.1 本构方程的建立 在金属热变形过程中,变形所需载荷主要取决 于材料的流变应力,因此精确的流变应力方程和本 构模型是描述材料热变形行为,以及进行塑性变形 数值模拟的基础。金属材料的热变形行为可理解为 位错借助外力和热激活作用来克服阻力而进行的运 动过程[10],变形过程受流变应力σ、应变ε、应变速 率ε · 和变形温度T 等4个因素的综合影响。采用 Arrhenius方程和Z(Zener-Hollomon)参数方程[11] 来研究试验钢的热变形行为,表达式为 ε ·=Aσ n1exp -Q RT (ασ <0.8) ε ·=A[exp(βσ)]exp -Q RT (ασ >1.2) ε ·=A[sinh(ασ)]nexp -Q RT (任何条件) ?? ?? ?? ???????? ???????? (1) Z =ε ·exp -Q RT (2) 式中:n1,n,A,α,β均为材料常数,其中α=β/n1;R 为气体常数,8.3145J·mol -1·K -1;Q 为热变形激 活能,kJ·mol -1。 在回归拟合较佳的条件下,由式(1)中双曲正弦 函数求得的材料常数与由幂函数和指数函数求得的 结果基本一致[12]。对式(1)中的幂函数和指数函数 形式方程两边取自然对数可得: lnε ·+ Q RT =lnA1 +n1lnσ (3) lnε ·+ Q RT =lnA2 +βσ (4) 对式(3)和式(4)两边进行偏微分可得: 1 n1 = ∂ lnσ ∂lnε · T (5) 1 β = ∂σ ∂lnε · T (6) 基于试验钢的峰值应力、真应变数据,根据式 (5)和式(6)得到lnσ和σ与lnε · 间的关系。由图3 (a)和图3(b)可知,lnσ、σ与lnε · 均呈线性关系,通 过拟合即可得到参数n1 为9.6718,β 为0.04325, α=β/n1=0.004472。 对式(1)中的双曲正弦函数形式方程两边取自 然对数可得: lnε ·+ Q RT =lnA +nlnsinh(ασ) (7) 对式(7)两边求导可得: 1 n = lnε · lnsinh(ασ) (8) Q =nR d lnsinh ασ d(1/T) (9) 根据式(8)和式(9),得到lnε · 和lnsinh(ασ)间 的关系以及lnsinh(ασ)与1000/T 间的关系,结果 83 廉晓洁:含硼不锈钢的热变形行为 如图3(c)和图3(d)所示,从而计算得到试验钢的热 变形激活能Q 为620.32kJ·mol -1。这与文献[13] 中304奥氏体不锈钢的激活能(486kJ·mol -1)相差 很大,由此可知添加一定量的硼元素可提高304不 锈钢的热变形激活能。热变形激活能是表征金属材 料变形难易程度的一个物理量,热激活能越大,表明 晶体中原子跳动的频率越低,相应的原子扩散速率 也越小,在宏观上表现为材料越难变形。 由式(1)和式(2)可得: Z =ε ·exp -Q RT =A sinh ασ n (10) 对式(10)两边取对数可得: lnZ =lnε ·+ Q RT =lnA +nlnsinh ασ (11) 根据式(11)拟合得到lnZ-lnsinh(ασ)曲线如 图3(e)所示,计算得到lnA 为55.3688,n 为6.7402。 因此,在试验范围内基于峰值应力构建的试验钢的 热变形本构方程为 ε ·=exp55.3688 sinh 0.004472σ 6.7402 × exp 620320 8.3145T (12) 高温变形条件下,与变形温度及应变速率相比, 变形量对应力的影响较小[14],因此大多数研究中不 考虑变形量的影响。可知,上述基于峰值应力所构 建的方程不能够准确地表征整个热变形过程中应力 的变化。为了更精确地表征含硼不锈钢在热变形过 程中的流变特征,利用以真应变为自变量的5次多 项式来拟合含硼不锈钢在不同真应变下的材料常数 α,Q,lnA,n,拟合曲线如图4所示,拟合结果如表1 所示。由图4可知,含硼不锈钢材料常数与应变的5 次多项式拟合相关系数均大于0.995,表明以变形量 为自变量的5次多项式能够很好地表征含硼不锈钢 材料常数的变化规律。根据双曲正弦函数定义,流变 应力可表征为Z 参数的函数,再结合5次多项式的拟 合结果,含硼不锈钢的本构关系可描述为 σ= 1 α ln Z A 1/n + Z A 2/n +1 ?? ?? ???? ?? ?? ???? 1/2 Z =ε ·exp Q RT α=C0 +C1ε+C2ε 2 +C3ε 3 +C4ε 4 +C5ε 5 Q =D0 +D1ε+D2ε 2 +D3ε 3 +D4ε 4 +D5ε 5 lnA =E0 +E1ε+E2ε 2 +E3ε 3 +E4ε 4 +E5ε 5 n=F0 +F1ε+F2ε 2 +F3ε 3 +F4ε 4 +F5ε 5 ?? ?? ?? ???????????? ???????????? (13) 

3.2 本构模型的验证 

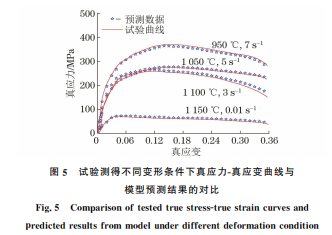
为验证所建立本构模型的准确性,另选取4组 工艺,即:950 ℃,7s -1;1050 ℃,5s -1;1100 ℃, 3s -1 和1150℃,0.01s -1 进行热压缩试验,将由试 验测得的真应力-真应变曲线与模型预测曲线进行 对比。由图5可知,随机选取的4组变形条件下的 试验数据和预测数据吻合较好,平均相对误差绝对 值仅为2.76%,这说明所建立的本构模型能够准确 预测含硼不锈钢的热变形行为。 84 廉晓洁:含硼不锈钢的热变形行为 材料常数 常数项 1次项系数 2次项系数 3次项系数 4次项系数 5次项系数 α 0.00998 -0.10516 0.96382 -5.0178 12.9447 -12.70825 Q 784.41796 -4750.28431 46032.01504 -241217.9802 614405.699 -595799.5978 lnA 76.28876 -525.35964 4230.71621 -17641.13261 36442.54549 -29714.87122 n 7.97875 -36.56308 336.08884 -1584.03999 3573.44042 -3055.99644 图5 试验测得不同变形条件下真应力-真应变曲线与 模型预测结果的对比 Fig.5 Comparisonoftestedtruestress-truestraincurvesand predictedresultsfrom modelunderdifferentdeformationcondition 

3.3 动态再结晶发生的临界条件 

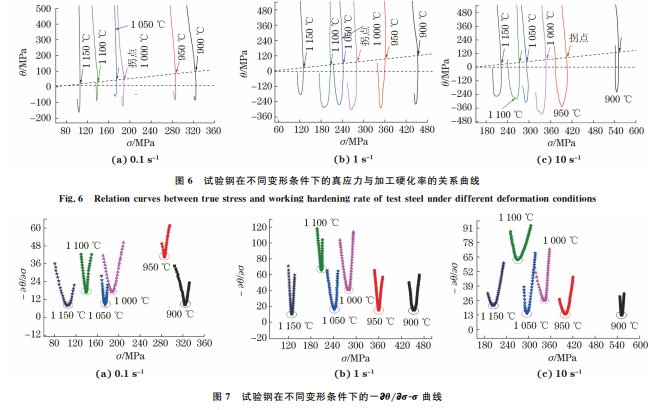
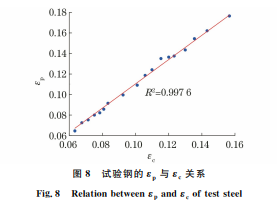
发生动态再结晶的临界应力可以通过确定θ-σ (θ为加工硬化率,θ= dσ dε )曲线或- ∂θ ∂σ -σ 曲线的 拐点或最小值来确定,其对应的真应变即为临界应 变[15-16]。由图6可知:试验钢在不同变形条件下的 加工硬化率均随着真应力的增加而减小,直至加工 硬 化率-真应力曲线出现拐点,此时由位错密度所积 蓄的能量达到最大,试验钢组织开始发生动态再结 晶,该拐点处所对应的真应力为临界应力σc,但这 时加工硬化率并不为零;随后加工硬化率继续减小, 直至为零,此时所对应的真应力为峰值应力σp。随 着变形温度的降低,试验钢的峰值应力增大。 由图7可知,在所有变形条件下,-∂θ/∂σ 均存 在一个最小值,其对应的真应力即为临界应力。随 着变形温度的增加或变形速率的减小,临界应力减 小,这表明在高温或低应变速率下变形,试验钢更容 易发生动 态 再 结 晶,这 与 HAN 等[17]的 研 究 结 果 一致。 临界应力和峰值应力对应的临界应变εc 和峰 值应变εp 的拟合曲线如图8所示。由图8可知:当 εp 较小时,εc-εp 数据点位于拟合直线的下方,即变 形温度较高、应变速率较小时,试验钢较易发生动态 再结晶;而当εp 较大时,εc-εp 数据点基本上位于拟 合直线的上方,即变形温度较低、应变速率较大时, 动态再结晶不易发生。由图 9 可知:在 1150 ℃, 1s -1 条件下热压缩后,当真应变为10%时,试验钢 85 廉晓洁:含硼不锈钢的热变形行为 图6 试验钢在不同变形条件下的真应力与加工硬化率的关系曲线 Fig.6 Relationcurvesbetweentruestressandworkinghardeningrateofteststeelunderdifferentdeformationconditions 图7 试验钢在不同变形条件下的-∂θ/∂σ-σ 曲线 Fig.7 -∂θ/∂σ-σcurvesofteststeelunderdifferentdeformationconditions 图9 试验钢在1150 ℃和1s -1 条件下热压缩不同真应变时的显微组织 Fig.9 Microstructuresofteststeelduringhotcompressionwithdifferenttruestrainsat1150 ℃ and1s -1 图8 试验钢的εp 与εc 关系 Fig.8 Relationbetweenεpandεcofteststeel 组织中出现了再结晶晶粒,此时热压缩试验过程中 的流变应力大于临界应力,这验证了计算结果的准 确性;随着变形量的进行,组织中形成了更多的再结 晶晶粒。 

4 结 论

 (1)在变形温度900~1150℃和应变速率0.1~ 10s -1 条件下热压缩后,含硼不锈钢的流变应力-应 变曲线为典型的动态再结晶型,软化机制以动态再 结晶为主;随着变形温度的升高或应变速率的减小, 试验钢的峰值应力及其对应的真应变降低。 (2)根据热压缩试验数据,基于 Arrhenius方 程并结合5次多项式拟合建立了含硼不锈钢的热变 形本构方程,且由方程计算所得的真应力-真应变曲 线与试验 测 得 的 相 吻 合,平 均 相 对 误 差 绝 对 值 为 2.76%,说明所建立的本构模型能够准确预测含硼 不锈钢的热变形行为。结合加工硬化率-真应力曲 86 廉晓洁:含硼不锈钢的热变形行为 线确定了含硼不锈钢发生动态再结晶的临界应力, 变形温度较高、应变速率较小时,该钢较易发生动态 再结晶。 

来源：材料与测试网