分享：直流电压降方法在钢材疲劳过载延迟效应研究中的应用

夏昊阳,吴 昊 

(同济大学航空航天与力学学院,上海 200092) 

摘 要:通过引入等效残余应力强度因子 ΔKres,提出了一种无材料拟合参数的新型驱动力模 型,对裂纹扩展速率与延迟疲劳寿命进行预测;采用直流电压降(DCPD)方法结合有限元标定测得 裂纹扩展长度,并与实测值进行比较,验证该方法的准确性;基于 DCPD 方法结合有限元标定通过 过载疲劳试验得到4种钢材过载后的裂纹扩展速率与延迟疲劳寿命,验证预测模型的准确性。结 果表明:单峰过载后,4种试验钢均出现过载延迟效应;过载比越大,试验钢过载后的最小裂纹扩展 速率越小,且屈服强度越低的试验钢的延迟效果越大。采用 DCPD 方法结合有限元标定得到的裂 纹扩展长度与实测值的相对误差小于3.75%,该方法具有较高的精度;驱动力模型预测得到的裂 纹扩展速率的变化趋势与由 DCPD方法结合有限元标定得到的试验值相吻合,且预测延迟疲劳寿 命均在试验值的2倍误差带内,验证了驱动力模型的准确性。

 关键词:驱动力模型;直流电压降;裂纹扩展速率;过载延迟效应;疲劳寿命 中图分类号:TG142.1 文献标志码:A 文章编号:1000-3738(2021)04-0088-06

0 引 言

 疲劳断裂是钢材常见的失效或破坏形式之一, 因为金属结构件尤其是钢材在实际使用中,常常承 受着变幅载荷。已有研究[1]发现,过载会导致裂纹 扩展的延迟,而预测变幅加载下的裂纹扩展速率是 88 夏昊阳,等:直流电压降方法在钢材疲劳过载延迟效应研究中的应用 非常具有挑战性的一项工作。Paris公式是预测宏 观裂纹扩展速率最常用的方法之一,该模型假设裂 纹扩展速率由应力强度因子幅值 ΔK 决定[2] ;但是 基于线弹性断裂力学的 Paris公式无法准确描述过 载延迟效应。近年来有非常多的学者对钢材的疲劳 过载延迟 现 象 进 行 了 研 究。根 据 裂 纹 闭 合 现 象, WOLF [3]定义了闭合率U 并给出了过载后的模型 公式;为 了 反 映 延 迟 效 应,WILLENBORG 等[4]提 出用延迟系数 Cp 来预测过载后的裂纹扩展速率; BACILA 等[5] 通 过 分 段 线 性 函 数 方 法 对 Willenborg模型进行了修正;WU 等[6]使用权函数 方法来量化残余应力强度因子并计算残余应力引起 的裂纹闭合效应,同时提出了适用于一些标准试样 的残余应力强度因子的计算公式[7] ;DAI等[8]提出 了一种以塑性修正后的应力强度因子为新的驱动力 来预测裂纹扩展速率的方法;YUEN 等[9]从裂尖塑 性区出发,考虑了材料特性对扩展行为的影响后提 出了一个改进的 Wheeler模型;HARMAIN [10]利用 裂纹闭合与裂尖塑性区的耦合效果来解释单峰过载 延迟现象,并给出了对应的计算公式。但是,上述方 法都需要针对不同材料进行试验以获取参数进行拟 合,应用限制非常大。 由于疲劳裂纹的测量通常在恶劣的动态环境中 进行,因此应用一个好的疲劳裂纹检测方法是非常 必 要 的。 其 中,直 流 电 压 降 (Direct Current PotentialDrop,DCPD)方法[11-12]是一种基于材料导 电性能的疲劳裂纹检测方法,该方法的优点包括:可 克服环境对测量过程的影响,即使在高温易腐蚀等 恶劣环境中也可进行测量;可通过温度补偿来消除 温度引起的误差;对噪声干扰不敏感;测量时通过改 变直流电的方向测量2次即可消除金属与导线的接 触电压;可测量小裂纹的萌生速率和裂纹扩展速率, 具有较高的精度。因此,DCPD 方法非常适合于具 有良好导电性能的钢材的疲劳裂纹研究。当恒定直 流电流穿过试样裂纹区域,裂纹长度的变化会改变 这段区间的电阻,从而改变2个探头之间的电势差, 因此 DCPD方法通过测量裂纹两侧直流电势差来反 映裂纹实时长度,进而得到裂纹扩展速率。目前,有 关 DCPD方法在钢材疲劳过载延迟效应研究中的应 用报道较少。作者通过引入等效残余应力强度因子 ΔKres,提出了一种无材料拟合参数的新型驱动力模 型,基于有限元标定辅助 DCPD方法,采用过载疲劳 试验对4种不同钢材过载后的裂纹扩展速率与延迟 疲劳寿命进行测试,验证了预测模型的准确性。 

1 新型驱动力模型的建立

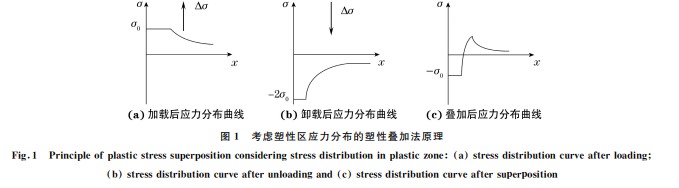
 在线弹性断裂力学中,裂尖拉伸应力σy 的计算 公式为 σy = ΔK 2πr cos θ 2 1+sin θ 2 sin 3θ 2 (1) 式中:r,θ为极坐标参数。 Rice在此基础上提出并应用塑性叠加法来计 算残余应力[13],即在卸载过程中,基于 Bauschinger 效应,反向屈服强度为2σ0(σ0 为屈服强度),叠加后 的残余应力σres 分布可由图1得到,图中 Δσ为加载 与卸载时所施加的力,x 为裂纹扩展方向的长度。 图1 考虑塑性区应力分布的塑性叠加法原理 Fig 1 Principleofplasticstresssuperpositionconsideringstressdistributioninplasticzone a stressdistributioncurveafterloading b stressdistributioncurveafterunloadingand c stressdistributioncurveaftersuperposition 基于权函数[6]提出的等效残余应力 σ-res 计算 公式为 σ-res =∫ rpl /W 0 σres x W F(a,W)? x W d x W (2) 式中:W 为试样宽度;a 为裂纹长度;rpl 为塑性区半 径;x 为沿裂纹扩展方向坐标;F(a,W)为权函数几何 函数;?(x/W)为与试样几何尺寸有关的权函数,该函 数为单调递减的正函数,且当x=0时,?(0)=1 [14]。 根据权函数要求,用满足要求的负指数函数作 为权函数?(x/W),得到: ? x W =exp -D x W (3) F(a,W)= 8 πD f(a/W) (4) 89 夏昊阳,等:直流电压降方法在钢材疲劳过载延迟效应研究中的应用 式中:D 为与试样类型和尺寸有关的无量纲拟合参 数,对于紧凑拉伸(CT)试样,由试验结果拟合得到 的D 取30;f 为 CT 试样的无量纲几何函数[15]。 将得到的?(x/W ),F(a,W )代入式(2),即可 得到等效残余应力。等效残余应力强度因子 ΔKres 的计算公式为 ΔKres =σ-res πa = 8π Da∫ rpl /W 0 σres x W exp -D x W d x W (5) 有效应力强度因子 ΔKeff 为应力强度因子幅值 ΔK 减去等效残余应力强度因子 ΔKres,即 ΔKeff=ΔK -ΔKres (6) 为了量化单峰过载后塑性区对疲劳寿命的影 响,将 ΔKeff 代入 Paris公式来预测裂纹扩展速率和 延迟疲劳寿命,计算公式为 da dN =C(ΔK -ΔKres)m Nd =∫ ad+a0 a0 1 (da/dN) da ?? ?? ?? ?????? ?????? (7) 式中:C,m 为 Paris公式参数;a 为裂纹长度;N 为 循环次数;da/dN 为裂纹扩展速率;Nd 为延迟寿 命;a0 为初始裂纹长度;ad 为裂纹扩展长度。

 2 试样制备与试验方法 

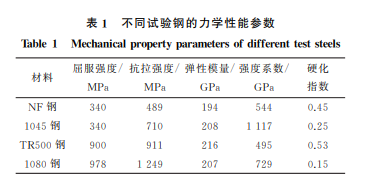
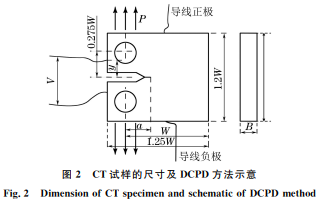
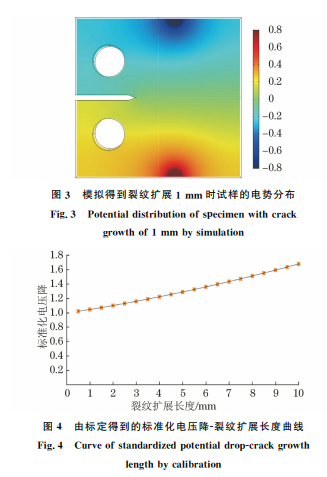
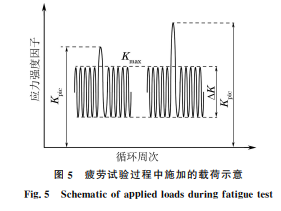
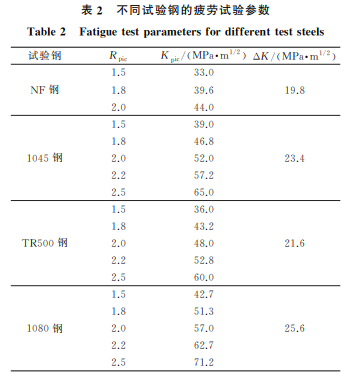
采用 DCPD方法对4种钢材的 CT 试样进行过 载疲劳试验以验证预测模型的通用性,这4种钢分 别为2种不同热处理态12NiCr6镍铬钢、1080高碳 钢和1045中碳钢。12NiCr6钢的化学成分(质量分 数/%)为 0.12C,1.6Ni,0.85Cr,0.76Al,0.6Mn, 0.32Si,热处理方式分别为880 ℃×1h正火处理和 880 ℃×1h水淬+500 ℃回火处理;将这2种热处 理态的 12NiCr6 钢分别记作 NF 钢和 TR500 钢。 1080高碳钢的化学成分(质量分数/%)为0.814C, 0.12Si,0.598Mn,0.122Cr,0.23Cu,0.014S,热处理 方式为815 ℃×1h油淬+480 ℃回火。1045中碳 钢的化 学 成 分 (质 量 分 数/%)为 0.47C,0.252Si, 0.717Mn,0.012P,0.005Mo,0.003S,热处理态为热 轧态。由拉伸试验测得试验钢的力学性能参数如 表1所示。 根据 ASTM E647,在试验钢上截取 CT 试样, 试样的厚度B 为15mm,宽度W 为80mm,初始裂 纹长度a0 为15mm,CT 试样的尺寸以及 DCPD测 定方法如图2所 示 。试 验 中 将 销 钉 插 入CT试 样 的 表1 不同试验钢的力学性能参数 Table1 Mechanicalpropertyparametersofdifferentteststeels 材料 屈服强度/ MPa 抗拉强度/ MPa 弹性模量/ GPa 强度系数/ GPa 硬化 指数 NF钢 340 489 194 544 0.45 1045钢 340 710 208 1117 0.25 TR500钢 900 911 216 495 0.53 1080钢 978 1249 207 729 0.15 圆孔中,向两端沿箭头所示方向施加载荷 P,在导 线中通入稳定的直流电,测定裂纹两端电势差V。 通过 DCPD 软件实时获取并储存循环次数及其对 应的应力强度因子、电势差等。由于 DCPD 试验过 程中输入的电流不变,所以电势差信号与裂纹长度 存在一定的函数关系,对于裂纹高度可忽略不计的 CT 试样,通常采用Johnson公式[16]计算裂纹长度, 该公式为 ΔV(a) V0(a0)= cosh -1[cosh(πy/2W)/cos(πa/2W)] cosh -1[cosh(πy/2W)/cos(πa0/2W)] (8) 式中:a 为裂纹长度;y 为2个探头间距离的一半; ΔV/V0 为标准化电压降;ΔV 为实时电压;V0 为初 始电压。 图2 CT试样的尺寸及 DCPD方法示意 Fig.2 DimensionofCTspecimenandschematicofDCPDmethod 利用Johnson公式计算裂纹长度一般会产生一 定的误差,因此需要采用有限元方法在试验前对探 头两端 测 得 电 势 差 与 裂 纹 长 度 进 行 标 定。 选 用 COMSOL软件进行有限元模拟,建立 DCPD 试验 模型,用参数扫描功能模型裂纹从初始长度a0 扩展 10mm 的过程,记录电势数据。模拟得到裂纹扩展 1mm(即裂纹长度为16 mm)时的电势分布,结果 如图3所示。 采用有限元仿真得到的不同裂纹长度及其对应 的两探头间的电势差,拟合得到裂纹扩展长度与标 准化电压降的关系曲线,结果如图4所示。根据标 定得到的标准化电压降-裂纹扩展长度曲线,即可由 DCPD方法测定的电势差得到实时的裂纹长度,从 90 夏昊阳,等:直流电压降方法在钢材疲劳过载延迟效应研究中的应用 图3 模拟得到裂纹扩展1mm 时试样的电势分布 Fig.3 Potentialdistributionofspecimenwithcrack growthof1mmbysimulation 图4 由标定得到的标准化电压降-裂纹扩展长度曲线 Fig.4 Curveofstandardizedpotentialdrop-crackgrowth lengthbycalibration 而计算出实时裂纹扩展速率。 图5 疲劳试验过程中施加的载荷示意 Fig.5 Schematicofappliedloadsduringfatiguetest 为尽量减少测试误差,在销钉和探针外露部分均 用绝 缘 胶 带 包 裹。为 了 使 试 样 在 加 载 频 率 为 15Hz时具有相同的标准塑性区尺寸,均采用应力比 R 为0.1的 ΔK 进行疲劳试验。在每次测试过程中 均对试样施加一个频率为0.1Hz的单峰过载,具体 如图5所示,图中 Kpic 为过载时的最大应力强度因 子,Kmax 为循环加载时的最大应力强度因子。表2 列出了不同试验钢的试验参数,表中Rpic 为过载率。 采用降应力强度因子法预制疲劳裂纹,即在裂纹萌生 阶段将 ΔKmax 从1.4ΔK 降到 ΔK。试样的初始裂纹 长度a0 为15mm,当裂纹长度到达18mm 时结束预 制,然后保持 ΔK 不变将裂纹扩展至长度为20mm, 随即施加单峰过载,再继续使用 ΔK 进行加载;当 DCPD软件显示的实时裂纹扩展速率为正常速率并 保持10000周次循环稳定后停止试验。 表2 不同试验钢的疲劳试验参数 Table2 Fatiguetestparametersfordifferentteststeels 试验钢 Rpic Kpic/(MPa·m 1/2)ΔK/(MPa·m 1/2) 1.5 33.0 NF钢 1.8 39.6 19.8 2.0 44.0 1.5 39.0 1.8 46.8 1045钢 2.0 52.0 23.4 2.2 57.2 2.5 65.0 1.5 36.0 1.8 43.2 TR500钢 2.0 48.0 21.6 2.2 52.8 2.5 60.0 1.5 42.7 1.8 51.3 1080钢 2.0 57.0 25.6 2.2 62.7 2.5 71.2 

 3 结果与讨论

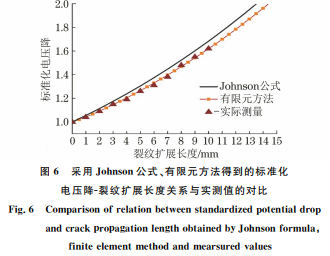
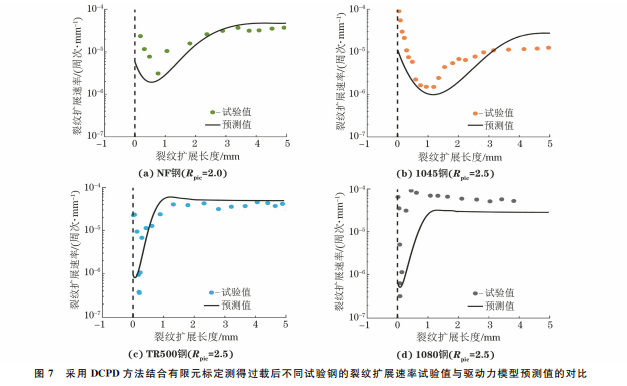
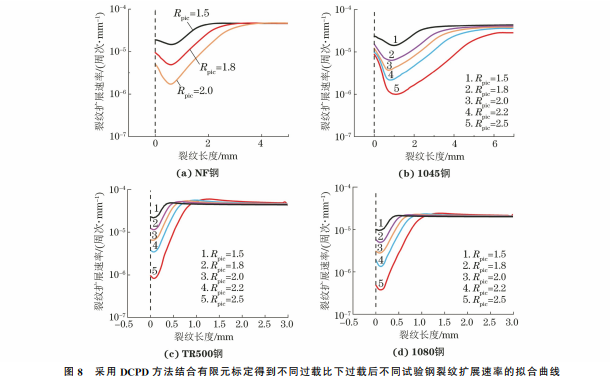
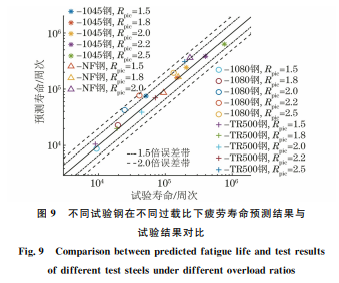
 由图6可以看出:由Johnson公式计算得到的 标准化电压降-裂纹扩展长度关系与试验结果存在 一定的误差,而使用有限元方法得到的裂纹扩展长 度 与 试 验 结 果 间 的 误 差 较 小,相 对 误 差 小 于 3.75%。由此可知,使用 DCPD 方法结合有限元标 定确定裂纹扩展长度的准确性与精度较高。 由图7可以看出,单峰过载后,4种试验钢的裂 纹扩展速率先下降到最低点后逐渐恢复到正常值, 该现象即为过载延迟效应。通过对比试验结果与模 型预测结果可以看出,裂纹扩展速率试验值与预测 值的变化趋势吻合度较高。其中,1080钢的裂纹扩 91 夏昊阳,等:直流电压降方法在钢材疲劳过载延迟效应研究中的应用 展速率预测值与试验值的偏差较大,出现该问题的 原因可能在于:(1)材 料 参 数 C,m 具 有 一 定 分 散 性,导致过载后的裂纹扩展速率预测值与试验值存 在较大的偏差;(2)图(1)所示的计算疲劳载荷下裂 尖塑性区的 Rice塑性叠加方法过于简化,无法真实 描述塑性 区 边 缘 形 状 与 塑 性 区 内 应 力 分 布,而 且 1080钢为高强度钢,裂尖塑性区较小导致应力梯度 过大,造成 Rice方法计算的σres(x/W )与实际结果 存在偏差。采用 DCPD 方法得到的试验数据非常 稳定,没有产生噪点,说明该方法在测量裂纹疲劳扩 展速率中有非常好的稳定性,且具有较高的准确性。 由图8可知:疲劳裂纹扩展速率的延迟效应主 图7 采用 DCPD方法结合有限元标定测得过载后不同试验钢的裂纹扩展速率试验值与驱动力模型预测值的对比 Fig.7 ComparisonbetweenexperimentalcrackgrowthrateafteroverloadingofdifferentteststeelsobtainedbyDCPDmethod combinedwithfiniteelementcalibrationanddrivingforcemodelpredictedvalues 图8 采用 DCPD方法结合有限元标定得到不同过载比下过载后不同试验钢裂纹扩展速率的拟合曲线 Fig.8 FittingcurvesofcrackgrowthrateafteroverloadingofdifferentteststeelsunderdifferentoverloadratiosobtainedbyDCPD methodcombinedwithfiniteelementcalibration 92 夏昊阳,等:直流电压降方法在钢材疲劳过载延迟效应研究中的应用 要由过载比决定,随着过载比的增大,试验钢在过载 后的延迟效应增大,过载延迟长度也增大,且屈服强 度较低试验钢的延迟效应影响长度远大于屈服强度 较高试验钢的。 由图9可以看出:除1080钢外的其他3种试验 钢的预测寿命都位于1.5倍误差带内,预测效果较 好;1080钢的部分预测寿命的误差偏大,但仍位于2 倍误差带内,这是因为材料参数与裂尖塑性区内应力 分布公式计算结果的偏差导致裂纹扩展速率预测结 果的偏差,进而造成预测寿命的偏差。综上可知,新 型驱动力模型的预测精度较高,适用性较广,同时验 证了 DCPD方法在过载延迟效应研究中的有效性。

4 结 论

 (1)单峰过载后,4种试验钢的裂纹扩展速率 先下降到最低点后逐渐恢复到正常值,试验钢出现 过载延迟效应;过载比越大,试验钢过载后的最小裂 纹扩展速率越小,且屈服强度较低试验钢的延迟效 果较大。由 DCPD 方法结合有限元标定得到的裂 纹扩展长度与实测值间的相对误差小于3.75%,说 明该方法具有较高的准确性,且在测量裂纹疲劳扩 展速率中有非常好的稳定性。 (2)采用新型驱动力模型预测得到裂纹扩展速 率的变化趋势与由 DCPD 方法结合有限元标定得 到的试验值相吻合,4种试验钢的预测延迟疲劳寿 命均位于2倍误差带内,新型驱动力模型的预测精 度较高,适用性较广。

来源：材料与测试网