分享：热塑性聚氨酯复合纤维布料拉伸过程的超弹性和黏弹性本构模型

薛厚庆,孙长乐,姜欣齐,胡 昊,杨继臣

(大连海事大学船舶与海洋工程学院,大连 116000)

摘 要:通过拉伸试验,分别考虑涂层的影响以及拉伸时间、拉伸速度、黏弹性应力与反作用力对初始应力的影响,建立了改进后的热塑性聚氨酯复合纤维布料及其单股纤维束的超弹性本构模型和黏弹性本构模型,预测了拉伸过程的应力-应变和应力松弛曲线,并与试验结果进行对比。结果表明:建立的超弹性本构模型能较准确地预测布料及其单股纤维束的应力-应变曲线,相对误差不超过3.5%;黏弹性本构模型能较准确地预测布料的应力松弛曲线,相对误差不超过3.21%。

关键词:TPU 复合纤维布料;应力-应变曲线;应力松弛;超弹性;黏弹性中图分类号:TB332 文献标志码:A 文章编号:1000-3738(2021)06-0057-05

0 引 言

热塑性聚氨酯(TPU)复合纤维布料具有质轻,抗拉强度高,柔软性、耐磨性、透气性好等特点[1],是一种理想的充气膜材料,可用于制造室外场馆、梁桁式海上应急滑梯等大型充气结构。TPU 梁、桁柱作为大型结构的主要承载部件,其充气伸长率是影响其结构稳定性与安全性的重要因素,因此 TPU 复合纤维布料的拉伸应力-应变特性研究很有必要。TPU 复合纤维布料由基布和涂层构成,基布采用高强度经、纬向纤维编织而成,基布两面涂敷聚氨酯涂层或饰面层。在加载过程中,布料表现出复杂的非线性力学特性,经向纤维与纬向纤维表现出各向异性[2]。并且,纤维与纤维之间存在复杂的相互作用,因此布料具有超弹性与黏弹性。GREEN等[3]采用 Maxwell超弹-黏弹性模型描述了聚硫类橡胶的黏弹性行为,该模型采用动能方程得到应力与应变、应力与时间关系的张量表达式。LAKSARI等[4]和 KHAJEHSAEID等[5]提出了引入对数的黏弹性本构模型,该模型可以用来表征压缩过程中与应力衰减速度相关的弹性材料大变形规律。57薛厚庆,等:热塑性聚氨酯复合纤维布料拉伸过程的超弹性和黏弹性本构模型FAHIMI等[6]采用应变能函数,利用径向和扭转变形模式来校核弹性轴套的材料参数。黏弹性布料的应变与应力对时间的依赖性可以通过恒定载荷下的蠕变试验和恒定变形下的应力松弛试验来测试,布料的材料参数也可采用蠕变和应力松弛试验来测定[7]。在 TPU 复合纤维布料充气过程中,布料的变形在圆柱半径方向不敏感,而在长度方向非常敏感,长度方向的变形会直接影响充气设备的稳定性和安全性。为此,作者对 TPU 复合纤维布料进行单轴拉伸试验,研究拉伸过程纤维布料的应力-应变特性。通过拉伸试验,将单轴拉伸时的应力-应变曲线分为超弹性和黏弹性两部分,得到应力-应变和应力松弛曲线,分别考虑涂层的影响以及拉伸时间、拉伸速度、黏弹性应力与反作用力对初始应力影响,对超弹性本构模型和黏弹性本构模型进行改进,采用改进后的模型分别预测应力-应变和应力松弛曲线,并进行试验验证。

1 试样制备与试验方法

1.1 试样制备

试验材料为上海创元公司生产的 TPU840-06型 TPU 复合纤维布料,基布材料为尼龙 6。采用STM3000型万能拉力机,在基布中机械剥离出单股经向和纬向聚氨酯纤维束。复合纤维布料中经向和纬向纤维束的密度分别为1.25,1.20 股·mm-1。在STM3000型万能拉力机上对分离出的经向和纬向纤维束进行单轴拉伸试验。由于纤维束硬度低,夹具的夹持力较大,纤维束容易受损,在纤维束的夹持端使用硅胶垫片。纤维束拉伸试样尺寸如图1所示。拉伸过程中纤维束的拉力端保持与拉伸方向垂直,拉伸速度为60 mm·min-1,逐渐加载至纤维束断裂,得到纤维束的应力-应变曲线。在拉伸过程中,经向纤维束出现崩断响声。图1 纤维束单轴拉伸试样尺寸Fig.1 Dimensionofuniaxialtensilesampleoffiberbundle在STM3000型万能拉力机上对整体布料分别沿经向和纬向进行单轴拉伸和定应变拉伸试验。由于 GB/T528-2009标准的适用范围为橡胶等匀质材料,而作者研究的布料为带涂层的织物,为了确保布料有 效 拉 伸 部 分 测 试 结 果 的 准 确 性,在 GB/T528-2009规定标准试件尺寸的基础上适度增大有效拉伸部分的宽度。单轴拉伸试样的尺寸如图2所示,试样形状为哑铃形,尺寸误差在0.2mm 以内。定应变拉伸试样的形状为矩形,尺寸为150 mm×30mm×0.6 mm。单轴拉伸和定应变拉伸的拉伸速度均为90mm·min-1,在拉伸过程中若夹持端断裂或表面出现损伤,则视为无效件。对于定应变拉伸试验,将布料沿经纬方向分别拉伸至极限应变的20%和50%,保持应变不变,测应力随时间的变化曲线,得到应力松弛曲线。图2 TPU复合纤维布料单轴拉伸试样尺寸Fig.2 DimensionofuniaxialtensilesampleofTPUcompositefabric

2 试验结果与讨论

2.1 宏观形貌

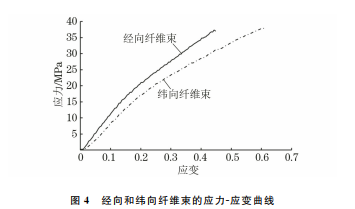
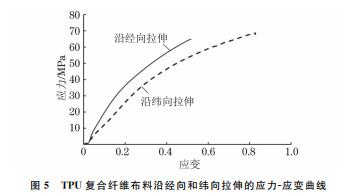
由图3可以看出,经向纤维束由一根根的纤维组成,推测拉伸过程中出现的崩断响声源于纤维断裂。图3 经向纤维束表面及剖面宏观形貌Fig 3 Surface a andprofile b macromorphologyofmeridionalfiberbundle2.2 应力-应变及应力松弛曲线由图4可以看出,单轴拉伸过程中,相同应力下纬向纤维束的应变略大于经向纤维束的,这是由于纬向纤维束在编织过程存在一定的卷曲度,而经向纤维束的卷曲度远远小于纬向纤维束的。由图5可以看出:应变相同时,复合纤维布料沿经向拉伸时的应力明显高于沿纬向拉伸时的,这是由于经向纤维束的密度略大于纬向纤维束的;布料沿纬向拉伸时的应变变化范围较沿经向拉伸时的58薛厚庆,等:热塑性聚氨酯复合纤维布料拉伸过程的超弹性和黏弹性本构模型图4 经向和纬向纤维束的应力-应变曲线Fig.4 Stress-straincurvesofmeridionalandzonalfiberbundles大,这是由于纬向纤维存在一定的卷曲度,拉伸时需要一定的拉力将纬向纤维拉直;布料沿纬向拉伸后的伸长率较纬向纤维束的大,这是由于复合纤维布料中,聚氨酯涂层对纬向纤维存在增强作用。图5 TPU复合纤维布料沿经向和纬向拉伸的应力-应变曲线Fig.5 Stress-straincurvesofTPUcompositefabricduringtesilealongmeridionalandzonaldirections由图6可以看出,TPU 复合纤维布料沿经向和纬向拉伸至应变分别为极限应变的20%和50%并保持此应变不变时,应力均发生了衰减。布料在拉伸过程中发生弹性变形和塑性变形,当发生塑性变形时,应力衰减。在两种定应变下,布料沿经纬方向的应力衰减程度相差不大,这是由于经纬方向纤维束的材料相同,编织规律相同,且应力衰减程度受纤维束密度的影响较小。

3 本构模型的建立与验证

3.1 超弹性模型

SPENCER[8]在均匀介质理论的基础上引入新的应变不变量I1~I5,得到拉伸过程复合纤维布料基布的超弹性本构模型,表达式为σij =I-1/23 FiRFjS∑5α=1Wα∂IαCRS+∂Iα CSR (1)C=FTF,Wα =∂W∂Iα(2)式中:σij 为基布从i位置变形到j位置时的应力;I3图6 在定应变分别为20%和50%极限应变下 TPU复合纤维布料沿经向和纬向的应力松弛曲线Fig.6 StressrelaxationcurvesofTPUcompositefabricalongmeridionalandzonaltensionatconstantstrainsof20%and50% ultimatestrain为第三应变不变张量,Iα 为第 α应变不变张量;F为变形梯度张量,FiR、FjS 为变形梯度张量的分量;Wα 为Iα 方向上的应变能;C 为右柯西格林张量,CRS、CSR 为右柯西格林应变张量的分量。在 TPU 复合纤维布料中,编织纤维的存在使得布料在拉伸过程的受力呈各向异性。单轴拉伸时,由于复合纤维布料的体积近似不变,I1 =0;同时,基布与聚氨酯涂层同时受力拉长,聚氨酯涂层可以使布料的强度增加,因此引入新的量I6 来表示拉伸过程中布料及聚氨酯涂层的应变不变张量。

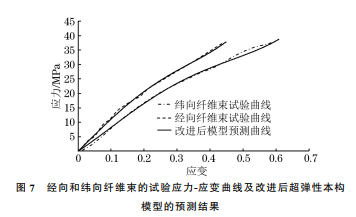
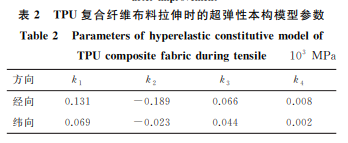
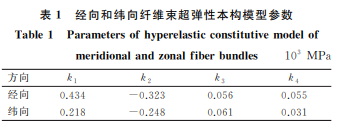
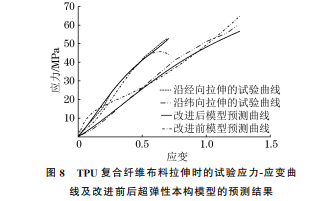
式中:σ为基布应力;B 为左柯西-格 林 张 量;a0 为经向纤维单位方向矢量;b0 为纬向纤维单位方 向矢量。由于布料为不可压缩材料,拉伸时,布料的厚度变小,纤维束的厚度与密度可近似为不变,因此式(3)中I2,I3,I6 的表达式分别为I2 =[(trC)2 -tr(C2)]/2 (4)I3 =detC=1 (5)59薛厚庆,等:热塑性聚氨酯复合纤维布料拉伸过程的超弹性和黏弹性本构模型I6 =1 (6)在拉伸方向,应变不变张量I4 的表达式为I4 =ε2 (7)式中:ε为应变。由于聚氨酯涂层可以增强基布的强度,用式(7)描述 TPU 复合纤维布料的超弹性并不准确。考虑涂层为各向同性材料,I4 可近似表示为I4 =ε2 -1 (8)由式(1)~式(6)及式(8)得到单轴拉伸条件下,改进后的超弹性本构模型表达式为σ=2(ε-1)×[k1(ε-1)3 +k2(ε-1)2 +k3(ε-1)+k4] (9)式中:k1 为拉伸时布料纤维与聚氨酯涂层的综合弹性系数,对布料非线性力学特性的影响最大;k2 为布料强度系数,主要受纤维束数量及其排列方式影响;k3 为与拉伸方向垂直的纤维束对布料强度的影响系数;k4 为纤维束与纤维束、基布与聚氨酯涂层的耦合摩擦因数。根据式(9),采用最小二乘法对经向和纬向纤维束的应力和应变数据进行拟合,得到经向和纬向纤维束超弹性模型中的各参数,如表1所示,则经向和纬向纤维束的超弹性本构模型表达式分别为σ=869.95ε4 -646.237ε3 +55.697ε2 +110.973ε (10)σ=437.799ε4 -496.313ε3 +122.106ε2 +74.539ε (11)由图7可以看出,改进后超弹性模型预测得到的经向和纬向纤维束的应力-应变曲线与试验应力应变曲线吻合,相对误差不超过3.3%,说明该模型的预测结果准确。表1 经向和纬向纤维束超弹性本构模型参数Table1 Parametersofhyperelasticconstitutivemodelofmeridionalandzonalfiberbundles 103 MPa方向 k1 k2 k3 k4经向 0.434 -0.323 0.056 0.055纬向 0.218 -0.248 0.061 0.031根据式(9),采用最小二乘法对复合纤维布料的应力和应变数据进行拟合,得到各参数如表2所示,则布料沿经向和纬向拉伸的超弹性本构模型表达式分别为σ=262.303ε4 -378.169ε3 +131.204ε2 +78.212ε (12)σ=13.955ε4 -46.282ε3 +38.673ε2 +41.753ε (13)图7 经向和纬向纤维束的试验应力-应变曲线及改进后超弹性本构模型的预测结果Fig.7 Teststress-strain curves of meridional and zonalfiberbundlesandpredictionbyhyperelasticconstitutive modelafterimprovement表2 TPU复合纤维布料拉伸时的超弹性本构模型参数Table2 ParametersofhyperelasticconstitutivemodelofTPUcompositefabricduringtensile 103 MPa方向 k1 k2 k3 k4经向 0.131 -0.189 0.066 0.008纬向 0.069 -0.023 0.044 0.002由图8可以看出,与改进前的超弹性本构模型相比,改进后超弹性本构模型预测得到的 TPU 复合纤维布料沿经向和纬向拉伸的应力-应变曲线与试验应力-应变曲线的吻合性更好,预测相对误差不超过3.5%,预测结果准确。图8 TPU复合纤维布料拉伸时的试验应力-应变曲线及改进前后超弹性本构模型的预测结果Fig.8 Teststress-strain curve and prediction by hyperelasticconstitutivemodelbeforeandafterimprovementofTPUcompositefabricduringtensile

3.2 黏弹性模型

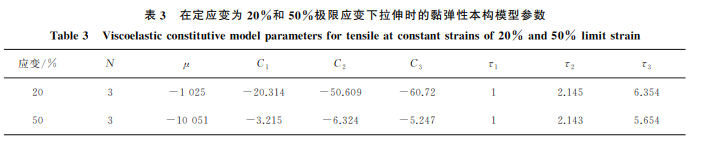
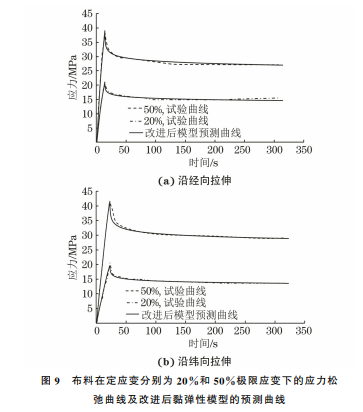
在拉伸过程中,材料会发生应力松弛。文献[9]用黏弹性模型来描述橡胶材料的应力松弛特性,表达式为σ(t)=σ0(ε)- ∑Nm=1cm ∫t0texp -t-t' τmdσ0(ε)dt'dt'????????????????????????(14)式中:t为拉伸时间;t0 为松弛时间;t'为衰减时间;σ(t)为拉伸时间为t时对应的应力;ε为应变;σ0(ε)60薛厚庆,等:热塑性聚氨酯复合纤维布料拉伸过程的超弹性和黏弹性本构模型为应变为ε 时的初始应力;cm 为材料系数;τm 为与拉伸时间有关的材料本构参数。式(14)将初始应力仅视为应变ε 的函数,并且忽略了拉伸过程中黏弹性应力与反作用力对布料应力松弛特性的影响。考虑应力松弛过程中拉伸时间及速度对初始应力的影响及黏弹性应力与反作用力对布料的影响,将黏弹性模型中的初始应力σ0(ε)转化为拉伸时间的函数,表达式为σ0(t)=μ∫t0∂σe∂δexp(δ-t)dδ (15)式中:μ 为拉伸时布料的弹性系数;σe 为瞬时应力,其值近似等于超弹性模型中的应力σ。联立式(14)、(15),得到改进后的黏弹性模型为σ(t)=μ∫t0∂σe∂δexp(δ-t)dδ-∑Ni=1c∫it0texp -t-t' τidσedt'dt' (16)根据式(16),采用线性差值法对 TPU 复合纤维布料的应力松弛数据进行拟合,得到黏弹性模型各参数,如表3所示。表3 在定应变为20%和50%极限应变下拉伸时的黏弹性本构模型参数Table3 Viscoelasticconstitutivemodelparametersfortensileatconstantstrainsof20% and50%limitstrain应变/% N μ C1 C2 C3 τ1 τ2 τ320 3 -1025 -20.314 -50.609 -60.72 1 2.145 6.35450 3 -10051 -3.215 -6.324 -5.247 1 2.143 5.654图9 布料在定应变分别为20%和50%极限应变下的应力松弛曲线及改进后黏弹性模型的预测曲线Fig 9 Stress relaxation curves and prediction of improvedviscoelasticmodeloffabricatconstantstrainsof20% and50% limitstrain a tensilealong meridionaldirectionand b tensilealongzonaldirection由图9和图10可以看出:在定应变分别为极限应变的20%和50%下,随着拉伸时间的延长,TPU复合纤维布料沿经向和纬向拉伸时的应力逐渐降低;应力衰减速度不随应变的增加而改变,但其衰减幅度随应 变 的 增 大 而 增 大;改 进 后 黏 弹 性 模 型 对图10 布料在定应变为50%极限应变下的应力松弛曲线及改进前后黏弹模型预测曲线Fig.10 Stressrelaxation curves and prediction of viscoelasticmodelbeforeandafterimprovementoffabricatconstantstrainof50%limitstrainTPU 复合纤维布料沿经纬向拉伸预测得到的应力松弛曲线与试验曲线的吻合较好,最大相对误差为3.21%,预测结果准确。

4 结 论

(1)与改进前的超弹性本构模型相比,考虑涂层对布料增强作用的改进后的超弹性本构模型能较准确地预测 TPU 复合纤维布料及单股纤维束拉伸过程的应力-应变曲线,相对误差不超过3.5%。(2)与改进前的黏弹性模型相比,考虑应力松弛过程中拉伸时间及速度,黏弹性应力与反作用力对初始应力影响的黏弹性模型对 TPU 复合纤维布料应力松弛曲线的预测结果更准确,与试验曲线的相对误差不超过3.21%。

来源：材料与测试网