分享:60钢热压缩变形行为及其变参数 Arrhenius本构方程
赵劲松1,周昌磊2,黄素霞2,李河宗2
(1.河钢集团邯钢公司大型轧钢厂,邯郸 056015; 2.河北工程大学河北省智能工业装备技术重点实验室,邯郸 056038)
摘 要:采用 Gleeble-1500 型热 模 拟 试 验 机 对 60 钢 进 行 不 同 温 度 (730,750,800,850,900, 1000 ℃)和不同应变速率(0.01,0.1,1,5,10s -1)的热压缩试验,总真应变为0.8,分析了60钢在热 压缩过程中的变形行为;引入变参数 Arrhenius模型,采用五阶多项式对模型中各参数随应变的变 化关系进行拟合,构建出60钢高温变形本构方程,并对方程的精确性进行了评估。结果表明:变形 温度越高,应变速率越低,60钢的流变应力越小;在较低温度和较高应变速率下,60钢热压缩变形 的软化机制主要为动态回复,在较高温度和较低应变速率下则主要为动态再结晶;建立的变参数 Arrhenius本构方程对流变应力的预测值与试验值的拟合相关系数达到0.994597,说明该本构方 程可以较好地描述60钢的高温变形行为。
关键词:60钢;热变形行为;变参数;Arrhenius本构模型 中图分类号:TG142 文献标志码:A 文章编号:1000-3738(2022)11-0086-06
0 引 言
60钢是一种碳质量分数在0.57%~0.65%的 碳素结构钢,广泛应用于电力钢缆、轮轴、家具弹簧 及各种垫圈等受力较大的高强度零件[1]。此外,60 钢还具有高硬度、高强度及低成本等优点,在耐磨钢 86 赵劲松,等:60钢热压缩变形行为及其变参数 Arrhenius本构方程 球方面有很好的应用前景。为了确定60钢的热加 工工艺参数,需要对60钢的高温塑性变形行为及其 影响因素进行研究。近年来,研究人员提出了多种 描述金属材料高温变形行为的本构方程,其中最典 型的一种是考虑变形温度和应变速率的 Arrhenius 本构方程。但是传统的 Arrhenius本构方程未考虑 变形程度 的 影 响,为 此 研 究 人 员 对 方 程 进 行 了 改 进[2-5],将方程中的各参数与应变相结合,考虑了应 变对流变应力的影响,得到了材料变参数流变应力 本构方程,从而获得了适用于42CrMo合金、TC20 钛合金、316LN 不锈钢等材料的更加精确的高温变 形应力-应变本构关系[5-7]。为了获得高硬度、低成 本耐磨60钢球的高温成形工艺,作者通过 Gleeble1500型热模拟试验机对60钢的高温变形行为进行 研究,构建了60钢变参数 Arrhenius本构方程,并 对方程进行了验证。


1 试样制备与试验方法
试验材料为某锻轧耐磨钢球厂试验用60钢,化 学成分 见 表 1。 将 试 验 钢 加 热 到 1100 ℃ 保 温 3min奥氏体化后,立即放入室温水中淬火得到的 热压缩变形前的初始显微组织,如图1所示。 表1 60钢的化学成分 Table1 Chemicalcompositionof60steel 元素 C Si Mn Cr S Ni Cu Fe 质量分数/% 0.57~0.65 0.17~0.37 0.5~0.8 <0.25 <0.035 <0.25 <0.25 余 图1 60钢热压缩变形前的原始显微组织 Fig.1 Originalmicrostructureof60steelbeforehot compressiondeformation 将试验材料加工成直径为8mm,高度为12mm 的圆柱形试样,在 Gleeble-1500型热模拟试验机上 进行单道次热压缩试验。试样以5 ℃·s -1的速率 加热到1100℃进行奥氏体化,保温3min,然后以 5 ℃·s -1 的 速 率 冷 却 至 变 形 温 度 (730,750,800, 850,900,1000℃),保温30s后,再分别以不同的 应变速率(0.01,0.1,1,5,10s -1)进 行 压 缩,压 缩 总真应变为 0.8,随 即 放 到 水 中 淬 火,以 保 留 变 形 后的组 织。为 了 避 免 加 热 及 变 形 过 程 中 金 属 氧 化,在氩气 保 护 下 进 行 热 压 缩 试 验。为 进 一 步 减 小摩擦的影 响,压 头 与 试 样 端 面 之 间 垫 有 涂 抹 二 硫化钼的 钽 片。试 验 过 程 中 的 载 荷、位 移、应 力、 应变、温度等 数 据 通 过 热 模 拟 试 验 机 的 计 算 机 系 统直接获取。 对热压缩后的试样进行镶嵌,依次采用400 # , 800 # ,1200 # ,2000 # 砂纸打磨,采 用 W1.5 金 刚 石 抛光膏进行抛光,采用体积分数4%硝酸酒精溶液 腐蚀后,在ICX41M 型 倒 置 光 学 显 微 镜 下 观 察 显 微组织。
2 试验结果与讨论
2.1 真应力-真应变曲线
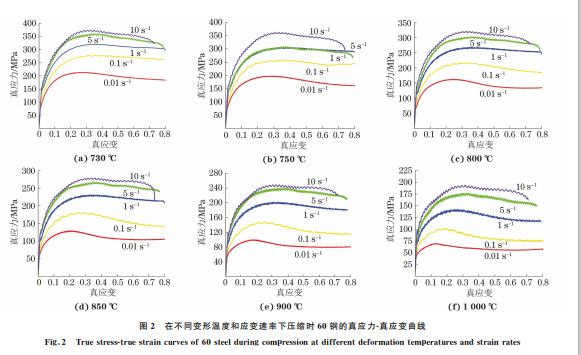
由图2可以看出:变形温度越高,应变速率越低, 60钢的流变应力越小,反之越大。在热压缩变形的 初始阶段,60钢的流变应力迅速增大,这是由于位错 增殖带来的加工硬化现象明显,软化机制来不及发挥 作用而导致的;随后随着变形的进一步增大,流变应 力缓慢增加直至峰值,此时晶粒内参与滑移的可动位 错数量增加,动态软化作用增强;流变应力在达到峰 值以后,随应变增加趋于平稳或者减小,这是因为60 钢进一步发生了动态再结晶,导致软化作用与加工硬 化相平衡甚至占主导地位。其中:在较高应变速率 (5,10s -1)和较低变形温度(730,750,800 ℃)下的软 化机制主要为动态回复,软化作用不明显,因此达到 峰值后的流变应力降幅较小;在较低应变速率(0.01, 0.1s -1)下,软化作用增强,流变应力下降趋势较明 显,特别是在较高变形温度下,降幅更加显著。这是 因为变形温度越高,原子的能量越高,越有利于原子 的运动及扩散,从而促进动态回复和动态再结晶的发 生;应变速率越小,变形的时间越长,动态再结晶就越 充分[8-9]。此外,在应变速率为10s -1 时,60钢的真 应力-真应变曲线呈现出比较明显的锯齿状波动,这 是由于压缩过快导致试样中的位错急剧增加,使晶界 周围产生新的形核,产生较强的动态回复软化,并且 软化作用与硬化作用交替进行。 87 赵劲松,等:60钢热压缩变形行为及其变参数 Arrhenius本构方程 图2 在不同变形温度和应变速率下压缩时60钢的真应力-真应变曲线 Fig 2 Truestress-truestraincurvesof60steelduringcompressionatdifferentdeformationtemperaturesandstrainrates 图3 在应变速率0.01s -1 不同变形温度下压缩至真应变为0.8时60钢的显微组织 Fig 3 Microstructuresof60steelaftercompressiontotruestrainof0 8atstrainrateof0 01s -1anddifferentdeformationtemperatures

2.2 显微组织
由图3可以看出:在850℃压缩变形后60钢的 显微组织相对于变形温度为800,750,730℃压缩变 形后粗大,存在明显的再结晶现象,且组织较均匀, 这与 图 2(d)显 示 的 明 显 的 软 化 现 象 相 一 致;在 800 ℃热压缩变形后显微组织没有明显的条带状变 形特征,出现了再结晶现象,与图2(c)显示的软化 现象相一致;在730 ℃热压缩变形后显微组织呈条 带状分布,表明压缩导致的变形晶粒未发生动态再 结晶,仍保持了变形形貌,这与图2(a)显示的软化 现象一致。因此,可以确定60钢的临界变形温度在 750 ℃左右。 88 赵劲松,等:60钢热压缩变形行为及其变参数 Arrhenius本构方程 图4 真应变0.5时60钢流变应力与应变速率和变形温度之间的关系 Fig 4 Relationshipbetweenflowstressandstrainrateordeformationtemperatureof60steelat0 5truestrain a relationshipoflnε ·-lnσ; b relationshipoflnε ·-σ; c relationshipoflnε ·-lnsinh ασ and d relationshipoflnsinh ασ -1/T
3 变参数 Arrhenius本构方程的建立及验证
3.1 变参数本构方程建立
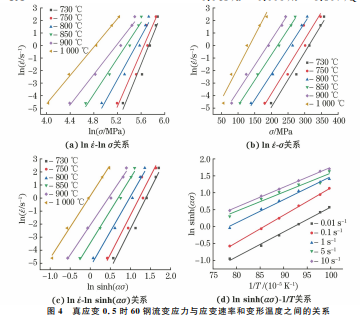
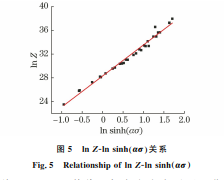
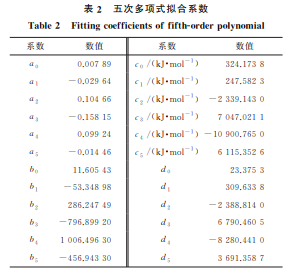
金属材料在热塑性变形时,其流变应力、应变速 率与温度之间的关系可由 Arrhenius本构方程[10-13] 表示: ε · = A1σ n0exp - Q RT (ασ <0.8) A2exp(βσ)exp - Q RT (ασ >1.2) A[sinh(ασ)]nexp - Q RT (任意应力水平) ?? ?? ?? ???????? ???????? (1) 式中:ε · 为应变速率;R 为气体常数;T 为热力学温 度;Q 为热变形激活能;σ为流变应力;A1,A2,A,n, n0,α,β均为材料参数,且β=n0α。 低应力水平(ασ<0.8)与高应力水平(ασ>1.2) 下流变应力、应变速率与温度之间的关系均可由任 意应力水平下的双曲正弦表达式表征。 金属材料在热塑性变形过程中,应变速率与变 形温度通过Z 参数影响应力和应变关系;Z 参数被 称为温度补偿应变速率因子[14-16],其表达式及与应 力之间的关系如下: Z =ε ·exp Q RT =A[sinh(ασ)]n (2) 由式(2)可得流变应力的表达式为 σ= 1 α ln ε ·expQ/(RT) A ?? ?? ???? ?? ?? ???? 1/n + ε ·expQ/(RT) A ?? ?? ???? ?? ?? ???? 2/n +1 (3) 对式(1)两边取自然对数,则有: lnε · =lnA1 - Q RT +n0lnσ (4) lnε · =lnA2 - Q RT +βσ (5) lnε · =lnA - Q RT +nlnsinh(ασ) (6) 对 于 某 一 给 定 变 形 温 度,Q 为 常 数,即 Q/(RT)为常数。将式(4)和式(5)求偏导,可以得 到该变形温度下的材料参数n0,β 分别为lnε ·-lnσ 和lnε ·-σ 直线的斜率。对于某一给定变形温度,将 式(6)两边求偏导,得到lnε ·-lnsinh(ασ)线性关系, 其斜率即为n 值。对于某一给定应变速率,将式(6) 对1/T 求偏导,lnsinh(ασ)-1/T 直线的斜率即为 Q/(nR)值,代入n和R 即可得到该应变速率下的热 变形激活能。按照上述思路,选择真应变ε为0.5 时的试验数据来计算60钢的材料参数,拟合得到 的各直线如图4所示,根据各直线斜率并结合β= n0α,R =8.314J·mol -1·K -1,得到n0 =8.333,β= 0.043,α=0.005,n=5.307,Q =297.509kJ·mol -1。 89 赵劲松,等:60钢热压缩变形行为及其变参数 Arrhenius本构方程 将变形温度、应变速率和相应的热变形激活能 代入式(2),即可得到相应变形条件下的Z 参数值, 再拟合出lnZ-lnsinh(ασ)的直线关系,如图 5 所 示,则该直线在lnZ 轴上的截距即为lnA 的值,由 此得到A=1.969×10 13。 图5 lnZ-lnsinh ασ 关系 Fig.5 RelationshipoflnZ-lnsinh ασ 将Q,n,α,A 值代入任意应力水平下双曲正弦 表达式,即可得60钢的 Arrhenius本构方程: ε ·=1.969×10 13[sinh(0.005σ)]5.307 × exp -297.509 RT (7) 将n,α,A 值代入式(3)中,则60钢在真应变为 0.5时的流变应力方程为 σ=200×ln ε ·exp 297.509 RT 1.969×10 13 0.188 + ?? ?? ?????? ε ·exp 297.509 RT 1.969×10 13 0.377 +1 ?? ?? ???????? (8) 由 Arrhenius本构方程可以直观地知道,流变 应力与应变速率和变形温度有关,并且流变应力还 与应变有关,是应变的函数。按照上述方法分别求 得真应变为0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8时60 钢的各材料参数值,采用五次多项式对各参数和真 应变进行拟合,拟合所用五次多项式为 α(ε)=a0 +a1ε+a2ε 2 +a3ε 3 +a4ε 4 +a5ε 5 n(ε)=b0 +b1ε+b2ε 2 +b3ε 3 +b4ε 4 +b5ε 5 Q(ε)=c0 +c1ε+c2ε 2 +c3ε 3 +c4ε 4 +c5ε 5 lnA(ε)=d0 +d1ε+d2ε 2 +d3ε 3 +d4ε 4 +d5ε 5 ?? ?? ?? ?????? ?????? (9) 式 中:α(ε),n(ε),A(ε) 为 随 真 应 变 变 化 的 Arrhenius本构方程材料参数;Q(ε)为随真应变变 化的热变形激活能;a0 ~a5,b0 ~b5,c0 ~c5,d0 ~ d5 为五次多项式系数。 各五次多项式拟合系数见表2,代入式(9)即得 到变参数α(ε),n(ε),A(ε),Q(ε)表达式。则60钢 的变参数 Arrhenius本构方程可表示为 σ= 1 α(ε) ln ε ·exp Q(ε) RT A(ε) ?? ?? ?????? ?? ?? ?????? 1 n(ε) + ε ·exp Q(ε) RT A(ε) ?? ?? ?????? ?? ?? ?????? 2 n(ε) +1 ?? ?? ?? ???? ???? (10) 表2 五次多项式拟合系数 Table2 Fittingcoefficientsoffifth-orderpolynomial 系数 数值 系数 数值 a0 0.00789 c0/(kJ·mol -1) 324.1738 a1 -0.02964 c1/(kJ·mol -1) 247.5823 a2 0.10466 c2/(kJ·mol -1) -2339.1430 a3 -0.15815 c3/(kJ·mol -1) 7047.0211 a4 0.09924 c4/(kJ·mol -1)-10900.7650 a5 -0.01446 c5/(kJ·mol -1) 6115.3526 b0 11.60543 d0 23.3753 b1 -53.34898 d1 309.6338 b2 286.24749 d2 -2388.8140 b3 -796.89920 d3 6790.4605 b4 1006.49630 d4 -8280.4410 b5 -456.94330 d5 3691.3587
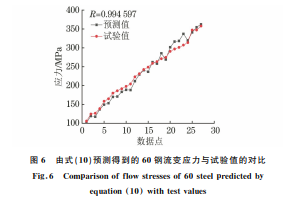
3.2 本构方程验证
由图6可知,由式(10)预测得到的流变应力和 试验值比较接近,相关系数R 达到0.994597,表明 所建立的变参数 Arrhenius本构方程能够较好地预 测60钢的流变应力。 图6 由式(10)预测得到的60钢流变应力与试验值的对比 Fig 6 Comparisonofflowstressesof60steelpredictedby equation 10 withtestvalues
4 结 论
(1)变形温度越高,应变速率越低,60钢的流 变应力越小,反之越大;在较高应变速率和较低变形 温度下,60钢热压缩变形的软化机制主要为动态回 90 赵劲松,等:60钢热压缩变形行为及其变参数 Arrhenius本构方程 复,在较高变形温度和较低应变速率下则主要为动 态再结晶。 (2)建立的60钢变参数 Arrhenius本构方程对 流变 应 力 的 预 测 值 与 试 验 值 的 相 关 系 数 达 到 0.994597,该 变 参 数 本 构 方 程 具 有 较 高 的 预 测 精度。
来源:材料与测试网







