分享：基于晶体塑性理论的 GH4169合金缺口效应研究

靖 雅,钟 飞,苑光健,曹 贤,王润梓,周帼彦,张显程

 (华东理工大学,承压系统与安全教育部重点实验室,上海 200237) 

摘 要:基于晶体塑性本构模型,通过生成宏观试样的代表性体积单元,对单轴拉伸和疲劳试验 数据进行拟合以获得满足模拟条件的相关参数,并分析了网格尺寸对模拟结果的影响;采用累积塑 性滑移和能量耗散作为指示因子进行疲劳裂纹萌生寿命预测,研究缺口尺寸对疲劳裂纹萌生寿命 的影响。

结果表明:采用所建立的模型获得的含缺口试样的疲劳裂纹萌生寿命在试验获得的疲劳 裂纹萌生寿命2倍误差带内,模型具有较好的预测精度;当缺口尺寸较小时,随着缺口尺寸的增加, 试样疲劳裂纹萌生寿命显著降低,当缺口尺寸大于临界缺口尺寸时,试样疲劳裂纹萌生寿命几乎不 受缺口尺寸影响。 

关键词:缺口效应;裂纹萌生寿命;晶体塑性模型;寿命预测 中图分类号:TB302 文献标志码:A 文章编号:1000-3738(2021)05-0084-07

0 引 言

 镍基合金 GH4169 由于强度高,蠕变性能、疲 劳性能和耐腐蚀性能良好,在航空发动机涡轮盘上 得到了广泛应用[1-2]。然而,强度和抗疲劳性能的提 高也可能提高缺口对疲劳载荷的敏感性[3],导致缺 口对疲劳寿命产生很大的影响。缺口效应主要在两 个方面影响疲劳寿命:一方面,应力集中容易出现在 缺口根部。AN 等[4]研究了应力集中对钢的缺口疲 劳行为的影响,认为应力集中严重影响疲劳性能,随 着 应 力 集 中 的 增 强,失 效 循 环 次 数 明 显 减 少; HUANG 等[5]也发现含缺口镍基合金的应力集中 导致其疲劳寿命显著降低,并且 U 形切口平板比 O 形切口平板具有更高的疲劳强度。另一方面,缺口 附近的晶粒取向对疲劳行为影响很大。不同的晶粒 取向会导致滑移面上的临界剪应力不同,疲劳裂纹 容易在高临界剪应力处萌生[6],从而影响疲劳寿命。 因此,含缺口材料的疲劳寿命敏感性较高。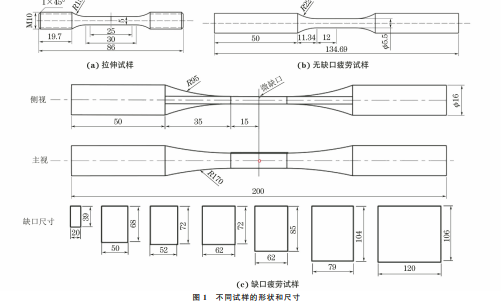这就有 必要通过介观尺度的晶体塑性模型,综合考虑缺口 尺 寸和局部晶粒取向的影响,对疲劳寿命进行更深 84 靖 雅,等:基于晶体塑性理论的 GH4169合金缺口效应研究 图1 不同试样的形状和尺寸 Fig 1 Shapeandsizeofdifferentsamples a non-notchedtensilesample b non-notchedsamplefor fatiguetestand c notchedsampleforfatiguetest 入的分析。 随着数值模拟技术的发展,基于显微组织对局 部损伤和裂纹扩展行为的模拟研究逐渐增多[7]。在 晶粒尺度上的力学行为评估通常利用晶体塑性理论 嵌入有限元获得应力应变演变而进行[8]。这种方法 可以有效地预测微观力学行为。与传统的宏观均匀 化模型预测方法相比,晶体塑性有限元法可以更好 地预测局部应力应变场,从而更有效地预测裂纹萌 生寿命。预测裂纹萌生寿命需要引入疲劳指示因 子,并将其与疲劳裂纹萌生相关的微观力学行为和 驱动力关联起来[7]。MANONUKUL 等[9]使 用 塑 性滑移作为疲劳指示因子,成功地评估了镍基高温 合金 C263的疲劳寿命;DUNNE 等[10]利用此疲劳 指示因子预测了疲劳裂纹萌生位置以及裂纹扩展行 为,模拟结果与试验结果能很好地吻合。因此,使用 疲劳指示因子可以较好地预测疲劳裂纹萌生及扩展 行为。然而,现有的研究大多集中于光滑试样疲劳寿 命的试验观察和数值模拟上,少见含缺口试样疲劳裂 纹萌生寿命预测的研究报道,尤其是鲜有基于晶体塑 性理论进行疲劳裂纹萌生寿命预测的研究报道。为 此,作者基于显微组织建立晶体塑性有限元模型,通 过光滑试样的单轴拉伸和疲劳试验确定模拟参数,采 用该模型预测了含缺口试样的疲劳裂纹萌生寿命,并 与试验结果进行对比,分析了缺口对裂纹萌生寿命的 影响,拟为缺口效应下的疲劳寿命预测提供参考。

 1 试样制备与试验方法 

试验材料为析出相强化材料 GH4169合金,由抚 顺特 殊 钢 股 份 有 限 公 司 提 供,平 均 晶 粒 尺 寸 为 10~20μm。在SX2-410型箱式电阻炉中对试验材料 进行固溶和时效热处理,以获得最优的力学性能。固 溶处理工艺为升温至960℃保温1h空冷,时效处理 工艺为升温到(720±5)℃,保温8h后,以50 ℃·h -1 的速率随炉降温至(620±5)℃,保温8h空冷。 使用 MTS伺服液压试验机进行单轴拉伸和疲 劳试验。单轴拉伸试验采用应变控制加载,拉伸速度 为0.6mm·min -1,拉伸试样为无缺口圆棒试样,尺寸 见图1(a)。疲劳试验分为2种:一种采用应变控制, 加载波形为三角波,应变比 Rε 为-1,应变速率为 8×10 -3s -1,应变幅为0.8%,试样为无缺口圆棒试 样,尺寸见图1(b);另一种采用应力控制,加载波形 为正弦波,最大名义应力为800MPa,频率为10Hz, 应力比R 为0.1,试样为缺口试样,尺寸见图1(c),缺 口通过激光加工制备[11]。为了消除激光加工造成的 微缺陷,降低表面粗糙度,用砂纸将缺口表面抛光至镜 面。用由50mLHCl+40mLH2O+10mLHNO3+ 85 靖 雅,等:基于晶体塑性理论的 GH4169合金缺口效应研究 2.5gCuCl2 组成的溶液腐蚀缺口表面。 无缺口试样单轴拉伸和疲劳试验的主要目的为 校准参数,含缺口试样疲劳试验的主要目的为研究 缺口对裂纹萌生寿命的影响。采用复型法获得含缺 口试样的裂纹萌生寿命,每隔一定循环次数后,中断 试验并施加80%最大水平应力的静态拉伸载荷,利 用复膜材料对缺口附近进行复型处理,并通过光学 显微镜观测缺口处的裂纹[12]。 

2 晶体塑性理论及有限元方法 

2.1 晶体塑性理论

 晶体塑性模型可以用来解释晶粒之间局部晶体 学响应。其中,晶粒的总变形和旋转可以用变形梯 度F [13]来表示,即: F =FeFp (1) 式中:Fe,Fp 分别为变形梯度中的弹性部分和塑性 部分。 塑性速率梯度Lp 与滑移系α 的塑性滑移速率 γ · α 相关[14],可以表示为 Lp =F · p(Fp)-1 =∑ N α=1 γ · αmα ??nα (2) 式中:mα,nα 分别为滑移系α 的滑移方向向量和滑 移法向向量;N 为总滑移数量。 塑性滑移速率的表达式为 γ · α =γ · 0exp - F0 kT<1- <τα -Bα -Sαμ/μ0 τ0μ/μ0 >p > ?? q ?? ???? ?? ?? ???? × sgn τα -Bα (3) 式中:k 为玻尔兹曼常数;T 为热力学温度;p,q 为 指数常数;γ · 0,F0,τ0 分别为参考应变速率、克服晶 格阻力所需的总自由能和晶格剪切应力;Bα,τα,Sα 分别为第α 个滑移系的背应力、分解切应力和滑移 阻力;μ,μ0 分别为温度在T 和0K 时的剪切模量。 定义<>为符号运算:当x>0时,=x;当x≤0 时,=0。 研究材料的疲劳行为,需要在本构模型中引入 随动硬化模型以考虑包辛格效应。通常用背应力的 演变[15]来量化随动硬化,第α 个滑移系的背应力演 化率B · α 可以表示为 B · α =hBγ · α -rDBα γ · α (4) rD = hBμ0 Sα μ'0 fcλ -μ -1 (5) 式中:hB 为硬化常数;rD 为与滑移阻力有关的动态 回复项:μ'0 为0K 时的局部滑移剪切模量;fc 为有 关内变量的耦合参数;λ 为介于0~1的比例因子。 第α 个滑移系的滑移阻力演化率S · α 方程可以 表示为 S · α =[hs -dD(Sα -S0)]γ · α (6) 式中:S0 为初始滑移阻力;hs,dD 分别为静态和动 态回复参数。 为了有效地评估和预测疲劳裂纹萌生寿命,在 本构模型中引入累积塑性滑移 P 作为疲劳指示因 子[9,16]。累计塑性滑移可以表示为塑性速率梯度 Lp 的方程,如下: P · = 2 3 Lp∶Lp 1/2 (7) P =∫ t 0 P · dτ (8) 式中:τ为时间。

 2.2 有限元模型 

2.2.1 代表性体积单元模型 

图2 GH4169合金的电子背散射衍射图和 RVE模型及其边 界条件示意 Fig 2 Electronbackscatterdiffractionimage a andillustration ofRVE modeland periodicboundarycondition b of GH4169alloy 由图2(a)可 见,GH4169 合 金 具 有 细 晶 结 构 和随机分布的晶粒取向。通过 Voronoi技术[17]建 立晶粒尺寸均匀平面应变代表性体积单元(RVE) 来表示宏观的材料 特 性,如 图 2(b)所 示,RVE 中 的平均 晶 粒 尺 寸 与 GH4169 合 金 晶 粒 尺 寸 相 符 (10~20μm)。其 中,种 子 布 局 采 用 随 机 分 布 策 略[16],并根据 图 2(a)的 结 果,赋 予 所 有 晶 粒 随 机 的3个欧拉角来表示宏观的随机取向。对于镍基 86 靖 雅,等:基于晶体塑性理论的 GH4169合金缺口效应研究 合金材料,当晶粒数量超过150个以后,模拟结果 会有较好的稳定性[18]。建立的 RVE 模型中 的 晶 粒数量大 于 200 个,因 此 该 模 型 具 有 代 表 性。周 期性边界条件为 uCD -uAB =uC -uA (9) vBD -vAC =vB -vA (10) 式中:uAB,uCD 为边线 AB 和 CD 在x 方向上的位 移;uC,uA 为节点 C 和 A 在x 方向上的位移;vBD, vAC 为边线BD和 AC在y 方向上的位移;vB,vA 分 别为节点 B和 A 在y 方向上的位移。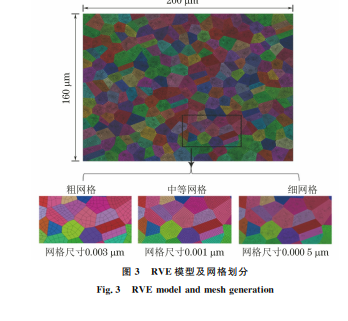 图3 RVE模型及网格划分 Fig.3 RVEmodelandmeshgeneration 设置的周期性边界条件会使对边之间形成平行 变形[19-20]。为了消除刚体运动的影响,将节点 A 在 x 和y 方向固定,将节点 B 和 C 在x 和y 方向固 定。另外,在节点 C施加位移载荷以模拟单轴应变 加载条件,采用平均法得到的宏观应力和应变响应 可表示为 σ- = 1 S∫S σdS (11) ε- = 1 S∫S εdS (12) 式中:σ-,ε- 分别为 RVE 模型的平均应力和平均应 变;S 为 RVE模型的总面积。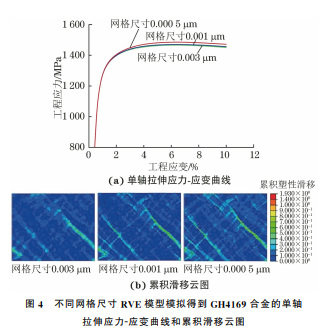 对 RVE模型划分网格,如图3所示,采用3种 尺寸(0.003,0.001,0.0005μm)的网格进行网格敏 感性研究。由图4可以看出,3种网格尺寸下均模 拟得到了相似的单轴拉伸应力-应变曲线和累积滑 移云图。因此,网格尺寸对仿真结果的影响可以忽 略不计。考虑到仿真精度和计算成本,选用尺寸为 0.001μm 的网格。 图4 不同网格尺寸 RVE模型模拟得到 GH4169合金的单轴 拉伸应力-应变曲线和累积滑移云图 Fig 4 Uniaxialtensilestress-straincurves a andaccumulated slipcontour b ofGH4169alloybysimulationwithRVE modelofdifferentmeshsize 

2.2.2 带有初始缺口的子模型 

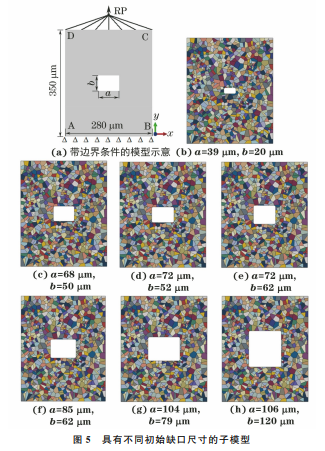
构建含初始缺口 RVE 模型,如图5所示,缺口 圆角半径统一为5μm,a 为缺口长度,b 为缺口宽 度。采用3种不同工况来避免微观结构和晶粒取向 图5 具有不同初始缺口尺寸的子模型 Fig 5 Sub-modelwithdifferentinitialnotchsize a illustration ofmodelwithboundaryconditionand b-h different initialnotchsize 87 靖 雅,等:基于晶体塑性理论的 GH4169合金缺口效应研究 的影响。通过两次随机赋予晶粒尺寸,使工况1和 工况2下的模型具有相同的微观结构和不同的晶粒 取向;将生成的两种微观结构赋予同一组晶粒取向, 使得工况1和工况3下的模型具有相同的晶粒取向 和不同的微观结构。由于含有缺口,因此无法使用 周期性边界条件。为了避免刚体运动的影响,底边 上的所有节点都受到y 方向上的约束,顶点 A 受到 x 方向的约束,约束条件如图5(a)所示,耦合 BC边 与参考点 RP,并在参考点 RP 施加集中载荷,载荷 条件 与 试 验 相 同。 最 大 主 应 力 800 MPa,频 率 10Hz,应力比0.1。

 3 结果与讨论

 3.1 材料参数的确定

 晶体塑性 本 构 模 型 参 数 包 括:弹 性 常 数 C11, C12,C44;与材料特性相关的参考应变速率γ · 0,总自 由能F0,晶格剪切应力τ0,指数常数p 和q;静态和 动态回复项的硬化参数hs 和dD 以及初始滑移阻 力S0;背应力参数中的硬化常数hB,0K 和 T 时的 剪切模量μ0 和μ,耦合参数fc,比例因子λ,0K 时 局部滑移剪切模量μ'0。 各向异性弹性常数计算公式为 C11 =E(1-ν)/[(1+ν)(1-2ν)] (13) C12 =Eν/[(1+ν)(1-2ν)] (14) C44 = Aa 2 (C11 -C12) (15) 式中:E 为弹性模量;ν为泊松比,取0.3;Aa 为各向 异性系数,取2.51 [21]。 由单轴拉伸试验获得试验材料的弹性模量为 198GPa。根据现有文献报道[9,18,21],γ · 0 在八面体 滑移系中为120s -1,在立方滑移系中为4s -1;F0 为295kJ·mol -1,λ 为0.85。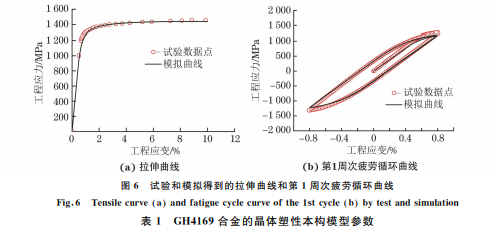其他参数通过试错法 结合拉伸曲线和第一周次的疲劳循环曲线确定,单 轴拉伸应力-应变曲线和疲劳循环1周次过程中的 应力-应变曲线试验结果和模拟结果见图 6。当试 验和模拟结果吻合时,所校准的参数才是可接受的。 由此确定立方体和八面体滑移系的材料参数,结果 如表1所示。 图6 试验和模拟得到的拉伸曲线和第1周次疲劳循环曲线 Fig 6 Tensilecurve a andfatiguecyclecurveofthe1stcycle b bytestandsimulation 表1 GH4169合金的晶体塑性本构模型参数 Table1 ParametersofcrystalplasticityconstitutivemodelforGH4169alloy 滑移系 C11/GPa C12/GPa C44/GPa p q ?0/MPa hs/GPa 八面体 267.09 114.47 191.54 0.31 1.8 810 513.00 立方体 267.09 114.47 191.54 0.99 1.6 1570 5.05 滑移系 dD/MPa S0/MPa hB/GPa μ0/GPa μ'0/GPa fc μ/GPa 八面体 6030 340 540 192 72.3 0.41 73.65 立方体 9 60 59 192 28.6 0.21 73.65

 3.2 基于塑性滑移的疲劳裂纹萌生寿命预测 

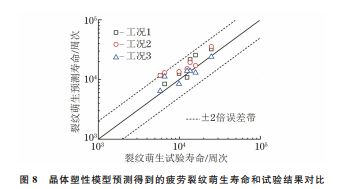
塑性滑移可用于预测裂纹萌生寿命。临界累积 塑性滑移pcrit 由试验中疲劳裂纹萌生寿命 Ni 和模 拟中每一周次的塑性滑移pcyc 来确定[9],二者之间 存在如下关系: pcrit =Nipcyc (16) 对于裂纹萌生占主导的失效模式[22],初始疲劳 寿命约等于失效寿命。因此,可用试验获取的寿命 数据来确定临界累积塑性滑移,计算得到临界累积 塑性滑移为118.2,然后再使用临界累积塑性滑移 来预测具有初始缺口子模型的裂纹萌生寿命。随着 疲劳循环周次的增加,不同工况下带初始缺口子模 88 靖 雅,等:基于晶体塑性理论的 GH4169合金缺口效应研究 型的临界累积塑性滑移也几乎呈线性增加,如图7 所示。因此,使用临界累积塑性滑移和每个循环周 次的塑性滑移来计算疲劳裂纹萌生寿命是合理的。 由图8可以看出,根据此方法预测的疲劳裂纹萌生 寿命数据点均落在2倍误差带之内,这表明此晶体 塑性模型具有良好的寿命预测能力。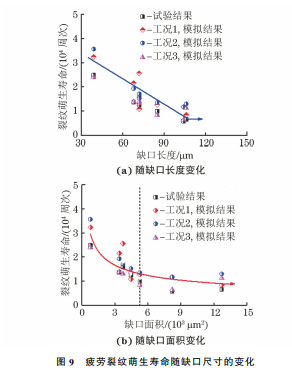 图7 带不同尺寸初始缺口子模型模拟得到累积塑性滑移随循环次数的变化曲线 Fig 7 Curvesofcumulativeplasticslipvsnumberofcyclesbysimulationwithsub-modelwithdifferentinitialnotches a condition1 b condition2and c condition3 图8 晶体塑性模型预测得到的疲劳裂纹萌生寿命和试验结果对比 Fig.8 Comparisonoffatiguecrackinitiationlifepredictedby crystalplasticitymodelandtestresults 3.3 缺口效应对疲劳裂纹萌生行为的影响 由图9(a)可知,随着缺口长度的增加,疲劳裂 纹萌生寿命呈线性降低趋势。这与 WANG 等[23]和 VINCENT 等[24]的研究结果类似。由图9(b)可知, 缺口面积A0 与疲劳裂纹萌生寿命之间存在反比例 关系,可以表示为 Ni= 516300 A 0.43 0 (17) 当初始缺口面积较小时,裂纹萌生寿命随着缺 口面积的增加迅速降低。但是,当初始缺口面积达 到某个特定值时,缺口面积的增加对裂纹萌生寿命 的影响不再明显。这可以通过裂纹扩展过程的3个 阶段来解释:微观短裂纹(第一阶段),宏观上的短裂 纹(第二阶段)和长裂纹(第三阶段)。当初始缺口尺 寸不超过微观短裂纹到宏观短裂纹的过渡点时,初 始缺口尺寸是影响裂纹萌生寿命的最重要因素;当 初始缺口尺寸接近微观短裂纹和宏观短裂纹过渡点 时,随着初始缺口尺寸增加,疲劳裂纹萌生寿命占总 寿命的比例减小,缺口尺寸对疲劳裂纹萌生寿命的 图9 疲劳裂纹萌生寿命随缺口尺寸的变化 Fig 9 Changesoffatiguecrackinitiationlifewithnotchsize a withnotchlengthand b withnotcharea 影响减弱;随着初始缺口尺寸的继续增加,疲劳长裂 纹阶段占据疲劳总寿命的大部分阶段,缺口尺寸效 应对长裂纹阶段寿命的影响可以忽略不计。因此, 当缺口 尺 寸 相 对 较 小 时 (小 于 临 界 缺 口 尺 寸,约 5200μm 2),其初始缺口尺寸对疲劳裂纹萌生寿命 影响很大;但当缺口尺寸很大时,其尺寸的增加对疲 劳裂纹萌生寿命的影响很小。

 4 结 论 

(1)通过单轴拉伸和疲劳试验获取晶体塑性本 89 靖 雅,等:基于晶体塑性理论的 GH4169合金缺口效应研究 构模型参数,建立 RVE 晶体塑性模型,模拟得到3 种网格尺寸下的单轴拉伸应力-应变曲线相似,说明 RVE模型的网格大小不影响模拟结果。 (2)采用临界累积塑性滑移预测得到缺口试样 的疲劳裂纹萌生寿命位于试验获得的疲劳裂纹萌生 寿命的2倍误差带之内,表明所用晶体塑性有限元 方法具有良好的寿命预测能力。 (3)当 缺 口 尺 寸 小 于 临 界 尺 寸 (缺 口 面 积 约 5200μm 2)时,缺口尺寸对疲劳裂纹萌生寿命有较 大的影响;大于临界尺寸时,缺口尺寸的增加对疲劳 裂纹寿命的影响很小

来源：材料与测试网