分享:基于压痕应变的不锈钢材料拉伸性能参数计算方法
薛 河,路景智,贾宇磊,王 双,王 正 (西安科技大学机械工程学院,西安 710054)
摘 要:建立连续球压痕试验三维有限元模型,通过单一变量法模拟了残余压痕应变与不同材 料拉伸性能参数(弹性模量90~210GPa、屈服强度180~300 MPa、应变硬化指数0.1~0.3)的关 系;在125组拉伸性能参数组合下进行连续球压痕试验有限元模拟,得到基于残余压痕应变的材料 拉伸性能参数计算公式并进行了试验验证。结果表明:残余压痕应变分别与弹性模量和屈服强度 存在对数线性关系,其对数与应变硬化指数之间存在幂律关系;将连续球压痕试验测得的316L不 锈钢的残余压痕应变代入材料拉伸性能参数计算公式,反演计算得到的弹性模量、屈服强度和应变 硬化指数与拉伸试验结果的相对误差分别为1.50%,1.57%,0.22%,说明基于残余压痕应变的不 锈钢材料拉伸性能参数计算方法可以满足工程需要。
关键词:残余压痕应变;有限元模拟;连续球压痕试验;拉伸性能参数 中图分类号:TG142.25;TH140.7 文献标志码:A 文章编号:1000-3738(2022)11-0092-05
0 引 言
工程结构中的许多部件都是通过焊接技术连接 起来的,如核电压力容器及管道等;焊接工艺的特点 使得焊接接头成为工程结构的薄弱区域[1],并且焊接 接头区域的力学性能会呈现出不均匀的特点[2],这就 92 薛 河,等:基于压痕应变的不锈钢材料拉伸性能参数计算方法 对局部材料力学性能的获取提出了更高的要求。通 过传统力学试验获取材料力学性能时,需要在待测部 位进行破坏性取样,且取样区域较大,难以对焊接接 头局部不同区域的力学性能进行准确分析[3]。微纳 米压痕试验作为一种无需取样的技术,因具有操作简 单、执行速度快、破坏性小等优势,已逐步成为测试在 役设备材料力学性能的重要方法[4-5]。 微纳米压痕试验起源于材料的硬度试验[6],经 发展和 改 进 后 被 用 于 测 试 材 料 的 硬 度 与 弹 性 模 量[7-8]。20世纪 80 年代初,HAGGAG 等[9-10]提出 了在被测材料同一点处进行多次加卸载循环的自动 化连续球压痕(ABI)测试技术。近年来,连续球压 痕测试 技 术 被 广 泛 用 于 测 试 金 属 材 料 的 力 学 性 能[11-13]。有学者通过连续球压痕试验测试了压力 容器用钢的拉伸性能参数,并通过与拉伸试验结果 进行对 比 验 证 了 该 方 法 的 可 行 性 与 准 确 性[14-16]。 关凯书等[17]通过引入损伤理论获得了连续球压痕 试验的塑性表征参数。瞿力铮等[18]采用三维建模 方法对典型幂硬化金属的连续球压痕试验进行模 拟,并对影响拉伸性能计算结果的因素进行了分析。 此外,XUE 等[19]采用连续球压痕试验结合有限元 反演分析,开发了一种获得不锈钢材料在不同伸长 率下应力-应变关系的方法。目前,连续球压痕测试 技术主要通过拟合无量纲方程来计算材料拉伸性能 参数,但由于加卸载过程中材料凹陷/凸起对压痕响 应参数的影响,计算误差较大。 为了建立更为准确的材料拉伸性能参数计算方 法,作者利用 ABAQUS软件建立三维有限元模型 模拟连续球压痕试验过程,通过单一变量模拟分别 建立弹性模量、屈服强度、应变硬化指数与残余压痕 应变的关系;在125组不锈钢拉伸性能参数组合下 对连续球压痕试验进行有限元模拟,建立了基于残 余压痕应变的不锈钢材料拉伸性能参数计算方法。
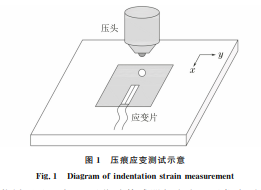

1 连续球压痕应变测试原理
在平面应力场中,当压头压入被测材料时材料 因受力而发生变形,由这种变形行为产生的应变变 化被称为压痕应变增量。当被测材料的力学性能发 生变化时,压头压入产生的压痕应变增量也会具有不 同的变化规律。因此,可以利用压痕诱导产生的压痕 应变增量对材料拉伸性能参数进行求解。如图1所 示,将电阻应变片粘贴于试样表面,在应变栅轴线中 心处控制压头沿垂直于试样表面方向以一定的速率 进行加卸载,每次加卸载构成一个循环;在每次加卸 图1 压痕应变测试示意 Fig.1 Diagramofindentationstrainmeasurement 载循环过程中,通过位移传感器与应变记录仪实时记 录不同压入深度下的压痕应变增量。建立连续球压 痕试验有限元模型,模拟得到压痕应变增量与材料拉 伸性能参数之间的对应关系,借助有限元反演分析将 压痕应变增量转化为材料的拉伸性能参数。 对于大多数不锈钢材料而言,其弹塑性行为可 以用幂律方程近似描述为 σ= Eε (σ ≤σy) Kε n (σ >σy) (1) 式中:σ为应力;E 为弹性模量;K 为强化系数;n 为 应变硬化指数;σy 为屈服强度;ε为总应变。 当σ>σy 时,式(1)可改写为 σ=σy 1+ E σy εp n (2) 式中:εp 为超过屈服阶段后不可恢复的塑性应变。
2 有限元模拟
采用 ABAQUS软件建立三维有限元模型模拟 连续球压痕应变测试过程,由于试样结构及所受载 荷具有对称性,故建立1/4模型。考虑到应变测试 的准确性,模型中试样尺寸设为10mm×10mm× 3mm,球形压头的直径为1mm。压头材料为碳化 钨,其弹性模量远大于被测材料,在压入过程中不会 发生变形,因此将其设置为刚体。 在压入过程中,试样的变形主要发生在与压头 接触的区域,而在远离压头的区域却几乎没有变形。 采用C3D8R网格单元进行网格划分,对靠近压头部 位的网格进行细化,如图2所示,最小网格尺寸为 0.025mm,从而保证压痕应变测试局部区域的响应 精度。对于非接触区域,网格单元尺寸随距压头距 离的增加逐渐增大。 边界条件设置为试样底面完全固定,在对称面上 施加对称性约束;对压头参考点施加位移载荷,使压头 只能沿垂直于试样表面的方向进行移动。设置5次加 93 薛 河,等:基于压痕应变的不锈钢材料拉伸性能参数计算方法 图2 有限元模型及网格划分 Fig.2 Finiteelementmodelandmeshgeneration 卸载循环,第一次循环时压入深度h 为0.10mm,第2 次为0.15mm,直至最大压入深度为0.30mm,加载 过程为准静态过程。材料模型选择 Hollomon幂硬化 本构模型,遵循 VonMises屈服准则。 金属材料具有弹塑性特性,在压头卸载之后会 发生一定程度的弹性恢复。设置了单一变量试验 组,具体不锈钢材料拉伸性能参数如表1所示。参 考 GB/T24179-2009,选择距压痕中心3mm 处作 为残余压痕应变的测试点,采用有限元模型模拟加 卸载过程,得到每次加卸载循环后测试点处的残余 压痕应变,分析残余压痕应变的变化规律。 表1 有限元模拟用不锈钢材料拉伸性能参数 Table1 Tensilepropertyparametersofstainlesssteel materialsforfiniteelementsimulation 编号 σy/MPa n E/GPa 试验 A 210 0.2 90,120,150, 180,210 试验 B 180,210,240, 270,300 0.2 210 试验 C 210 0.1,0.15,0.2, 0.25,0.3 210
3 基于残余压痕应变的材料拉伸性能参数 计算方法
3.1 弹性模量与残余压痕应变的关系
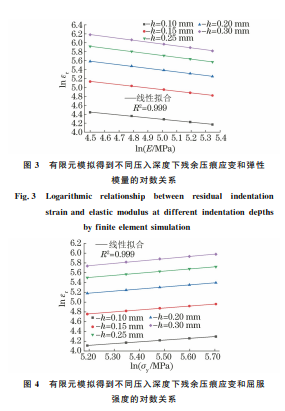
由图3可以看出:当屈服强度与应变硬化指数 为定值时,相同压入深度下,弹性模量越大,残余压 痕应变越小,弹性恢复能力越强;残余压痕应变与弹 性模量的对数之间存在良好的线性关系,其线性拟 合相关系数R 2 为0.999,拟合公式为 lnεr =a1lnE +a0 (3) 式中:εr 为残余压痕应变;a0,a1 为拟合系数。
3.2 屈服强度与残余压痕应变的关系
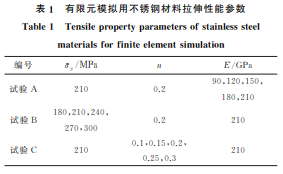
由图4可以看出:当弹性模量与应变硬化指数 为定值时,相同压入深度下,随屈服强度增加,残余 压痕应变增大,说明材料发生变形后保留塑性变形 图3 有限元模拟得到不同压入深度下残余压痕应变和弹性 模量的对数关系 Fig.3 Logarithmic relationship between residual indentation strainandelasticmodulusatdifferentindentationdepths byfiniteelementsimulation 图4 有限元模拟得到不同压入深度下残余压痕应变和屈服 强度的对数关系 Fig.4 Logarithmic relationship between residual indentation strainandyieldstressatdifferentindentationdepthsby finiteelementsimulation 的能力增强;不同压入深度下屈服强度与残余压痕 应变的对数同样具有明显的线性关系,线性拟合相 关系数为0.999,拟合公式为 lnεr =b1lnσy +b0 (4) 式中:b0,b1 为拟合系数。
3.3 应变硬化指数与残余压痕应变的关系
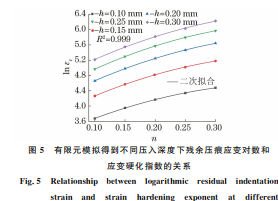
图5 有限元模拟得到不同压入深度下残余压痕应变对数和 应变硬化指数的关系 Fig.5 Relationship between logarithmic residual indentation strain and strain hardening exponent at different indentationdepthsbyfiniteelementsimulation 由图5可以看出:当弹性模量与屈服强度为定 值时,相同压入深度下,应变硬化指数越大,残余压 94 薛 河,等:基于压痕应变的不锈钢材料拉伸性能参数计算方法 痕应变越大;不同压入深度下残余压痕应变的对数 与应变 硬 化 指 数 呈 幂 律 关 系,拟 合 相 关 系 数 为 0.999,拟合公式如下: lnεr =c2n 2 +c1n+c0 (5) 式中:c0,c1,c2 为拟合系数。
3.4 材料拉伸性能参数计算方法的建立
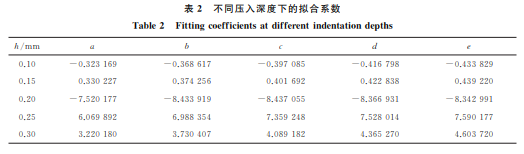
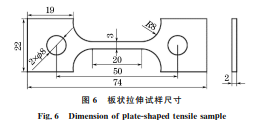
结合式(3)~式(5),即可建立残余压痕应变与 弹性模量、屈服强度和应变硬化指数的关系式: lnεr =alnE +blnσy +cn 2 +dn+e (6) 式中:a,b,c,d,e为拟合系数。 在试验参数范围,即弹性模量90~210GPa、屈 服强度180~300 MPa、应变硬化指数0.1~0.3范 围内,共有125种不同拉伸性能参数组合。在每组 拉伸性能参数下进行5次加卸载连续球压痕试验的 有限元模拟,得到不同压入深度下的残余压痕应变。 采用式(6)对材料拉伸性能参数和不同压入深度下 的残余压痕应变进行拟合,得到不同压入深度下的 拟合系数,如表2所示;将这些系数代入式(6),再代 入由连续球压痕试验测定的材料残余压痕应变,即 可反演计算得到材料的拉伸性能参数。 表2 不同压入深度下的拟合系数 Table2 Fittingcoefficientsatdifferentindentationdepths h/mm a b c d e 0.10 -0.323169 -0.368617 -0.397085 -0.416798 -0.433829 0.15 0.330227 0.374256 0.401692 0.422838 0.439220 0.20 -7.520177 -8.433919 -8.437055 -8.366931 -8.342991 0.25 6.069892 6.988354 7.359248 7.528014 7.590177 0.30 3.220180 3.730407 4.089182 4.365270 4.603720 4 试验验证 以山西太钢不锈钢有限公司提供的316L 不锈 钢薄板为研究对象。按照 GB/T4340.1-1999,在 卷板机上将316L不锈钢薄板轧制成2mm 厚的薄 板试样,再利用线切割法加工成板状拉伸试样,尺寸 如图6所示。利用 PLD-50型疲劳拉伸试验机进行 单轴拉伸试验,拉伸速度为2mm·min -1,进行3次 重复试验,取3次试验结果的平均值作为材料拉伸 性能参 数。试 验 测 得 316L 不 锈 钢 的 弹 性 模 量 为 205.2GPa,屈服强度为248.8MPa,应变硬化指数为 0.1360。 图6 板状拉伸试样尺寸 Fig.6 Dimensionofplate-shapedtensilesample 为避免试样翘曲对试验结果造成影响,截取板 状拉伸试样的标距段,镶嵌后进行表面抛光处理,直 至试样表面没有明显划痕,在其表面粘贴 BX120- 3AA 型应变片。将粘贴有应变片的试样放置在刚 性支座上,确保试验载荷垂直于试样表面,在改造的 UTM2000型电子万能试验机上进行连续球压痕试 验,压入过程采用位移控制,下压速度为0.1 mm· min -1,共进行5次加卸载过程,卸载率为50%,整 个加载过程为准静态,每次加卸载循环时的压入深 度与有限元模拟时一致,即第一次循环时压入深度 为0.10mm,第2次为0.15mm,直至最大压入深度 为0.30mm。利用 DH3818Y 型静态应变测试仪实 时监测试样表面的应变,记录不同压入深度下压痕 产生前后的应变差值(即残余压痕应变),共进行3 次连续球压痕试验取平均值。将不同压入深度下的 残余压痕应变代入式(6),反演计算得到316L 不锈 钢的拉伸性能参数并取平均值。由计算结果可知, 316L不锈钢的弹性模量为208.3GPa,屈服强度为 252.7MPa,应变硬化指数为0.1357,与拉伸试验结 果的相对误差分别为1.50%,1.57%,0.22%。相对 误差均保持在2%以内,说明基于残余压痕应变的 不锈钢材料拉伸性能参数计算方法可以满足工程 需要。
5 结 论
(1)建立连续球压痕试验三维有限元模型,通 过单一变量法模拟得到不锈钢材料残余压痕应变随 弹性模量增加而降低,随屈服强度或应变硬化指数 的增大而提高;残余压痕应变分别与弹性模量和屈 服强度存在对数线性关系,残余压痕应变对数与应 变硬化指数之间存在幂律关系。 (2)根据由单一变量法得到的各关系式,建立 95 薛 河,等:基于压痕应变的不锈钢材料拉伸性能参数计算方法 不锈钢材料的残余压痕应变与弹性模量、屈服强度 和应变硬化指数关系式,在125组不同不锈钢材料 拉伸性能参数下进行连续球压痕试验有限元模拟, 拟合得到基于残余压痕应变的不锈钢材料拉伸性能 参数计 算 公 式。 通 过 连 续 球 压 痕 试 验 测 定 得 到 316L不锈钢的残余压痕应变,再反演计算得到的弹 性模量、屈服强度、应变硬化指数与拉伸试验结果的 相对误差分别为1.50%,1.57%,0.22%,相对误差 均保持在2%以内,说明基于残余压痕应变的材料 拉伸性能参数计算方法可以满足工程需要。
来源:材料与测试网







