分享：N80Q钢的低周疲劳特性及寿命预测

崔 璐1,吴 鹏1,杨程晖1,康文泉1,李 臻1,魏文澜1,王 澎2

(1.西安石油大学机械工程学院,西安710065;2.蜂巢动力系统(江苏)有限公司,扬中212214)

摘 要:在Instron8862型疲劳试验机上对油井套管用N80Q钢进行完全对称循环载荷(平均应变为0)和非对称循环载荷(平均应变为0.5%和1.0%)下的低周疲劳试验,研究该钢的低周疲劳特性,并讨论了考虑不同因素的低周疲劳寿命模型的预测精度。结果表明:塑性应变能随应变幅的增大呈线性增长趋势,平均应变对塑性应变能几乎无影响;在对称载荷、不同应变幅(0.5%~2.0%)下以及非对称载荷、应变幅大于1.0%下,N80Q钢均无应力松弛行为,而在非对称载荷、应变幅小于1.0%时出现明显的应力松弛行为,且初始平均应力越大,应力松弛行为越明显;考虑最大应力、应力范围、应变范围以及平均应变影响的经验模型的预测精度较高,预测寿命主要分散在1.2倍分散带内。

关键词:低周疲劳特性;平均应变;应力松弛;疲劳寿命预测中图分类号:TG115.5 文献标志码:A 文章编号:1000-3738(2021)09-0073-06

0 引 言

在石油天然气的勘探开发过程中需要消耗大量的油井管。随着能源需求和钻井技术的发展,油井管的服役环境越来越恶劣,油井管的破坏往往伴随着巨大的经济损失[1-2],而疲劳失效是油井管最主要的破坏形式之一。井深的增加导致了井内压力和温度相应升高,油井套管在该服役环境下承受着超过材料屈服强度的拉/压应力循环作用,而蠕变和预应变的存在使得油井套管处于拉/压应变不等的状态,在上述多因素的作用下油井套管承受着非对称低周疲劳破坏的风险[3-4]。大量研究表明,材料的低周疲劳特性对疲劳寿命有着不可忽视的影响,在寿命预测模型中对影响疲劳寿命的因素进行修正能够有效提高寿命预测精度。MORROW 等[5]基于 Manson-Coffin方程提出了考虑平均应力影响的 Morrow 模型,大幅提高了73崔 璐,等:N80Q钢的低周疲劳特性及寿命预测疲劳寿命的预测精度;OHJI等[6]研究了2024铝合金在考虑平均应变下的疲劳损伤累积,并基于此建立了考虑应变比影响的寿命预测模型;张孝忠等[7]研究发现,考虑平均应力松弛的SWT 模型能够显著提高材料的疲劳寿命预测精度。随着工业技术的发展,结构部件的服役工况更加恶劣,平均应变对结构疲劳寿命的影响更加明显,因此该方面的研究得到广泛的关注。Morrow弹性修正模型、SWT修正模型以及 Walker修正模型等均通过平均应力修正来提 高 寿 命 预 测 精 度[8-10];苏 运 来 等[11] 基 于Manson-Coffin方程提出考虑应变比影响的新寿命预测模型,新模型对 CC450不锈钢、SAE1045钢以及GH4133高温合金疲劳寿命的预测结果较准确。平均应 变 也 会 对 平 均 应 力 松 弛 行 为 产 生 影 响。ELLYIN等[12]研究发现,在应变幅为0.515%时,平均应变越大,平均应力松弛速率越大;TAO等[13]研究发现,随着平均应变比的增加,材料的平均应力松弛速率增大。目前,有关井管材料在非对称载荷下的低周疲劳行为的研究较少。作者在不同平均应变下对油井套管用 N80Q 钢进行低周疲劳试验,研究了 N80Q钢的低周疲劳特性,基于此讨论了考虑不同因素的低周疲劳寿命模型的预测精度,分析了平均应变对疲劳断口和断裂特征的影响。

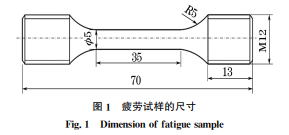
1 试样制备与试验方法

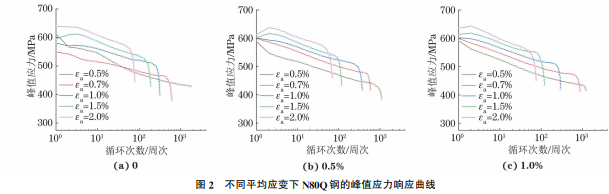
试验材料为N80Q套管钢,热处理工艺为890℃淬火30min+650℃回火1h,组织为回火索氏体,化学成分如表1所示。表1 N80Q钢的化学成分 质量分数Table1 ChemicalcompositionofN80Qsteel massfraction %C Si Mn P S Cr Mo Ni V Nb0.26 0.24 1.27 0.015 0.0076 0.04 0.01 0.02 0.003 0.006图2 不同平均应变下N80Q钢的峰值应力响应曲线Fig.2 PeakstressresponsecurvesofN80Qsteelunderdifferentmeanstrainsandstrainamplitude按照 GB/T15248-2008,在试验钢上沿轴向截取如图1所示的疲劳试样。为了研究平均应变对低周 疲 劳 行 为 的 影 响,采 用 应 变 控 制 方 式,在Instron8862型疲劳试验机上进行对称循环(平均应变εm 为0)和非对称循环载荷(平均应变εm 为0.5%和1.0%)下的3组低周疲劳试验,每组应变幅εa 分别为0.5%,0.7%,1.0%,1.5%,2.0%。试验温度为室温,波形为三角波,应变速率为0.004s-1。图1 疲劳试样的尺寸Fig.1 Dimensionoffatiguesample破坏准则为峰值拉应力下降至最大循环载荷的75%。疲劳试验结束后,采用 TESCAN VEGA 型扫描电镜(SEM)观察疲劳断口形貌。

2 试验结果与讨论

2.1 峰值应力响

应由图2可以看出:N80Q 钢的低周疲劳行为具有明显的循环软化特性;非对称循环载荷下的峰值应力响应呈现相似的特性,即在较大应变幅(1.5%和2.0%)下,N80Q 钢在疲劳初始阶段均有轻微的硬化行为,随即进入稳定软化阶段,最后峰值应力迅速下降直至试样断裂,而当应变幅小于1.5%时,N80Q钢直接进入软化阶段,最后试样失稳断裂,在对称循环载荷下当应变幅为0.5%时,N80Q钢没有出现应力失稳现象,而是直接断裂,其他应变幅下的74崔 璐,等:N80Q钢的低周疲劳特性及寿命预测峰值应力响应与非对称循环载荷下的相似。

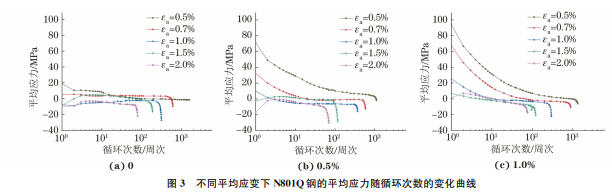
2.2 循环应力松弛特性

由图3可以看出:在对称循环载荷、不同应变幅下 N80Q钢均未出现应力松弛行为,平均应力保持在0左右;在非对称循环载荷下,应变幅小于1.0%时,N80Q钢出现了明显的应力松弛现象,且应变幅越小,初始平均应力越大,应力松弛越明显,而应变幅大于1.0%时,平均应力的变化趋势与对称循环载荷下的相同,未出现明显的应力松弛行为。大量研究[14-16]表明:应力松弛行为主要归因于循环塑性应变;最大拉伸应变εmax 由应变幅εa 和平均应变εm 组成,也可以分解为弹性应变εe 和塑性应变εp,可知随着平均应变的增大,材料的循环塑性应变增大,从而导致了明显的应力松弛行为。在发生初始硬化的应变幅下N80Q钢均未发生应力松弛。在循环加载过程中,具有循环硬化特性材料的循环塑性应变减小且总应力增大,因此应力松弛现象不显著[17]。图3 不同平均应变下N801Q钢的平均应力随循环次数的变化曲线Fig.3 CurvesofmeanstressvscyclenumberofN80Qsteelunderdifferentmeanstrains

2.3 滞回曲线

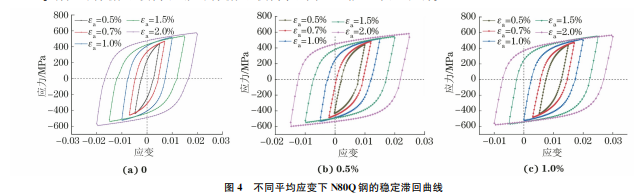
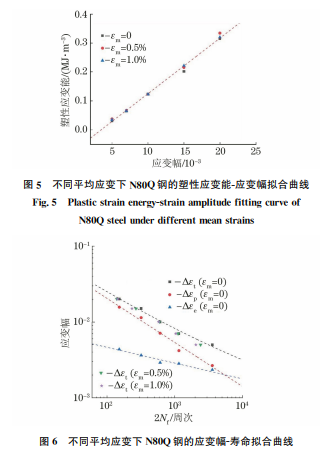
当材料受到超过其屈服强度的循环载荷作用时,应力-应变曲线会因材料发生塑性变形而形成封闭的滞回曲线。滞回曲线的面积表征的是材料的塑性应变能,代表每次循环后材料的能量损失。在破坏材料所需能量一定的条件下,滞回曲线的面积越大,材料发生疲劳破坏的寿命 Nf 越短[18]。图4为N80Q钢在对称循环载荷和非对称循环载荷、不同应变幅下0.5Nf 时的滞回曲线。由图4可以看出:在对称循环载荷下,N80Q钢的循环应力、应变满足Ramberg-Osgood关系式[19];随着平均应变的增大,滞回曲线整体沿拉伸应变的正方向平移;同一平均应变下的滞回曲线面积随着应变幅的增加而增加。由图5可以看出,N80Q 钢的塑性应变能与应变幅呈线性关系,平均应变对循环0.5Nf 时的塑性应变能几乎无影响。

2.4 寿命预测模型

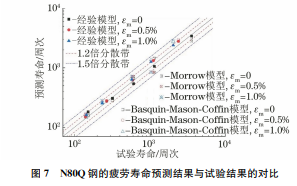
应变幅-寿命曲线是一种重要的材料性能曲线,广泛用于估算结构寿命[20]。图6中 Δεt/2为总应变幅,Δεp/2为塑性应变幅,Δεe/2为弹性应变幅。由图6可以看出,随着应变幅的增大,疲劳寿命呈指数缩短,平均应变对疲劳寿命的影响也变小。分别建立弹 性 应 变 幅、塑 性 应 变 幅 与 反 转 疲 劳 寿 命(2Nf)的指数关系模型,其中弹性应变幅与反转疲劳寿命的关系由Basquin模型拟合[21],而塑性应变幅与反转疲劳寿命的关系用 Manson-Coffin方程来描述[22],其关系式分别为Δεe/2=σ'fE(2Nf)b (1)Δεp/2=ε'f(2Nf)c (2)75崔 璐,等:N80Q钢的低周疲劳特性及寿命预测图5 不同平均应变下N80Q钢的塑性应变能-应变幅拟合曲线Fig.5 Plasticstrainenergy-strainamplitudefittingcurveofN80Qsteelunderdifferentmeanstrains图6 不同平均应变下N80Q钢的应变幅-寿命拟合曲线Fig.6 Strainamplitude-lifefittingcurvesofN80Qsteelunderdifferentmeanstrains式中:σ'f 为疲劳强度系数;b为疲劳强度指数;E 为弹性模量;ε'f 为疲劳延性系数;c为疲劳延性指数。利用Basquin-Manson-Coffin公式,得到总应变幅的计算公式为Δεt2=Δεe2+Δεp2=σ'fE(2Nf)b +ε'f(2Nf)c (3)拟合低周疲劳试验得到的总应变幅与反转疲劳寿命的关系即可预测低周疲劳寿命,拟合参数如表2所示。MORROW 等[5]基于平均应力对疲劳寿命的影响提出了 Morrow模型,表达式为Δεt2=σ'f-σmE(2Nf)b +ε'f(2Nf)c (4)式中:σm 为平均应力。表2 N80Q钢的Basquin-Manson-Coffin方程拟合系数Table2 FittingcoefficientsofBasquin-Manson-CoffinequationforN80Qsteelσ'f b ε'f c E/GPa2434.1 -0.2078 0.2955 -0.5801 202将表2中的数据代入式(4)即可得到 Nf=f(σm,εt)的关系式。陈宏等[23]提出了一种考虑最大应力、应力范围、应变范围以及应变比的低周疲劳寿命预测经验模型,表达式为σmaxΔσΔε 1-Rε =αNβ (5)式中:σmax 为最大应力;Δσ 为应力范围;Δε为应变范围;Rε 为应变比;N 为疲劳循环次数;α和β为材料参数。将应变比转变为平均应变和应变幅的函数后,即可得到经验模型:σmaxΔσΔε2εaεm +εa=αNβ (6)由图7可以看出:经验模型对 N80Q 钢疲劳寿命的 预 测 精 度 高 于 Morrow 模 型 和 BasquinManson-Coffin模型;Basquin-Manson-Coffin模型未考虑平均应力和平均应变的影响,因此该模型对非对称循环载荷下低周疲劳寿命预测的准确性较差;虽然 Morrow模型考虑了平均应变对低周疲劳寿命的影响,但是由于 N80Q 钢的应力松弛行为受到应变幅和平均应变两个方面的影响,因此其预测寿命较为分散,主要集中在1.2倍分散带和1.5倍分散带之间;经验模型考虑了最大应力、应力范围、应变范围以及平均应变的影响,预测寿命主要分散在1.2倍分散带内,该模型具有较高的预测精度。3个模型对较短疲劳寿命的预测较准确,预测精度随着寿命的延长而降低。这说明在应变幅大于1.0%时,应变幅对疲劳寿命的影响占主导地位;而在应变幅小于1.0%时影响疲劳寿命的因素较多,需要综合考虑各影响因素才能较准确地预测N80Q钢的低周疲劳寿命。

2.5 疲劳断口形貌

由图8可以看出,应变幅为1.0%时N80Q钢在不同平均应变下的疲劳断口均主要包括裂纹源区、裂纹扩展区和瞬断区。疲劳裂纹均从试样表面萌生,平均应变为0,0.5%时断口表面均存在两处裂76崔 璐,等:N80Q钢的低周疲劳特性及寿命预测纹源,N80Q钢发生多裂纹源扩展,断口表面存在明显的由多个扩展区交汇形成的撕裂台阶;平均应变为1.0%时 N80Q钢发生单一裂纹扩展。平均应变为0时,断口中存在大量脆性解理面,且脆性特征区域面积较大,疲劳条纹宽度分布在25~40μm 之间;在脆性解理面周围出现少量的韧性特征区域,脆韧区域交替出现表明断裂形式为周期性解理断裂,裂纹扩展方式为穿晶扩展;脆韧交替边界有少量细小的二次裂纹,二次裂纹的扩展方向与疲劳条纹的扩展方向一致,即垂直于疲劳裂纹扩展的方向。平均应变为0.5%时,断口中的脆性特征区域面积小于平均应变为0时的,疲劳条纹宽度主要分布在10~25μm之间,而韧性特征区域的面积较大;断口中出现尺寸较长的二次裂纹,裂纹扩展方式为穿晶扩展。平均应变为1.0%时断口中存在大面积明显的韧窝,而脆性解理面区域极少;与平均应变为0时的相比,二次裂纹的尺寸较小,数量较少;裂纹扩展方式为穿晶扩展。平均应变为0时,N80Q 钢以脆性解理断裂为主,随着平均应变的增加断裂特征逐渐向韧窝转变,周期性解理面面积减小,韧性穿晶断裂成为主要的断裂方式。研究[24]表明:在交变载荷较低时试样一般出现单一裂纹源,而在较高的交变载荷下则易出现多裂纹源;这是由于在疲劳载荷下试样发生塑性变形,位错运动诱发金属表面产生驻留滑移带,裂纹在驻留滑移带萌生。超过材料屈服强度的低周疲劳载荷使得试样表面产生多处驻留滑移带,从而导致多裂纹源扩展;但是在应变幅为1.0%、平均应变为1.0%的疲劳载荷下,较大拉伸应变导致试样表面缺陷处产生较大的应力集中,造成裂纹易在缺陷处萌生,因此N80Q钢发生单一裂纹扩展。

3 结 论

(1)N80Q钢在不同平均应变下的低周疲劳行为均具有明显的循环软化特性,塑性应变能与应变幅呈线性关系,且不受平均应变的影响;在对称循环载荷、不同应变幅下以及非对称循环载荷、应变幅大于1.0%下,N80Q 钢均无应力松弛行为,而在非对称循环载荷、应变幅小于1.0%时N80Q钢发生明显的应力松弛,且初始平均应力越大,应力松弛行为越明显;随着应变幅的增大,疲劳寿命呈指数减小,平均应变对疲劳寿命的影响程度减小。(2)考虑最大应力、应力范围、应变范围以及平均应变影响的经验模型的预测精度高于 Morrow模型和Basquin-Manson-Coffin模型,预测寿命主要分散在1.2倍分散带内。在应变幅大于1.0%时,应变幅对疲劳寿命的影响占主导地位,而在应变幅小于1.0%时影响疲劳寿命的因素较多。(3)当应变幅为1.0%,平均应变为0时,N80Q77崔 璐,等:N80Q钢的低周疲劳特性及寿命预测钢的断裂特征以脆性解理为主,随着平均应变的增加断裂特征逐渐向韧窝转变,周期性解理面面积减小,韧性穿晶断裂成为主要的断裂方式。

来源：材料与测试网