分享：球压痕试验法评价金属材料的强度

黄礼洋,关凯书 (华东理工大学,承压系统与安全教育部重点实验室,上海 200237) 

摘 要:通过单次压痕试验与有限元模拟相结合的方法,结合反向分析方法与模拟退火粒子群 算法,从获得的载荷-深度曲线加载部分提取材料的塑性参数,基于 Ludwig硬化模型预测了不同 金属材料的强度,并与单轴拉伸试验结果进行对比。结果表明:模拟得到的载荷-深度曲线与试验 得到的几乎重合,二者的相对误差小于0.5%,说明模拟退火粒子群算法可有效地从压痕载荷-深度 曲线中提取出金属材料的塑性参数;基于 Ludwig硬化模型,利用反向分析方法从压痕载荷-深度 曲线中提取的真应力-真塑性应变曲线不是唯一的,但从真应力-真塑性应变曲线计算得到的强度 具有明显的收敛趋势;采用压痕试验得到不同金属材料的强度均接近于由拉伸试验得到的,屈服强 度与抗拉强度的最大相对误差分别为5.9%,4.3%,说明采用压痕试验法可以准确地评价金属材料 的强度。 

关键词:压痕试验法;反向分析法;金属材料;屈服强度;抗拉强度 中图分类号:TG115.5 文献标志码:A 文章编号:1000-3738(2021)01-0085-07

0 引 言

 强度是材料的基础力学性能,该性能对压力容 器的设计及结构完整性的评估至关重要[1]。强度通 常是由常规拉伸试验获得的,在测试过程中需要制 备标准的拉伸试样,但是在试样较小或者无法取样 的情况下则难以进行该测试。为了解决这一难题, 压痕试验法应运而生。压痕试验是从硬度试验发展 而来的,其试验过程是将一个标准的压头压入被测 材料表面,同时记录下压入材料的深度和对应的载 荷[2]。通过分析得到的载荷-深度曲线,得到材料的 85 黄礼洋,等:球压痕试验法评价金属材料的强度 力学性能。压痕试验方法具有微损或者无损的特 性,被测材料表面仅有一个小于压头尺寸的凹坑残 留;压痕试验操作简单,不需要另外取样,可对在役 设备进行现场测试;利用该方法可以测得材料的多 种力学性能[3-7]。因此,压痕试验方法具有广阔的应 用前景。 目前,各国学者对采用压痕试验获得材料强度 进 行 了 广 泛 研 究,并 提 出 了 不 同 的 方 法。 TABOR [2]通过表征应力应变法获得金属材料的强 度,该方法需要准确地确定压头与试样的接触面积, 这是因为压头附近材料的堆积-沉陷现象会严重影 响测试结果的准确性[8] ;一次压入过程只能获得一 个表征应力-应变点,因此需要多个压入过程以累积 足够数量的表征应力-应变点。在 TABOR 提出的 方法基础上,为了更加方便地获得表征应力-应变 点,FILED等[9]通过压痕试验得到的卸载曲线计算 压头与试样的接触面积,并采用多次加卸载方式累 积足够数量的表征应力-应变点;该试验方法也称为 连续压痕法,广泛用于表征应力-应变点的测量,但 该方法需进行多次加卸载试验,操作比较繁琐。 随着计算机技术的发展,反向分析方法得到了 研究者的青睐。反向分析方法通常结合最优化算 法,将模拟获得的载荷-深度曲线逐步逼近试验测得 的曲线,进而提取出相应的应力-应变曲线,最终计 算出材料的强度[10]。但是由于多条应力-应变曲线 对应相似的载荷-深度曲线,因此需要结合额外的试 验信息才能得到唯一的应力-应变曲线,如压痕形 貌[11]、卸载曲线的斜率[12]、能量变化[13]等。如何通 过单次压痕试验的载荷-深度曲线获得准确的金属 材料强度,仍是目前研究的难点与热点。模拟退火 粒子群算法是智能优化算法的一种,结合了粒子群 算法和模拟退火算法的优点,能够快速搜索到全局 最优解。传统粒子群优化算法虽然能够快速搜索到 最优解,但是容易陷入局部收敛。模拟退火算法则 在搜索过程中具有概率突跳的能力,能够有效避免 搜索过程中陷入局部最优值。粒子群算法和模拟退 火算法结合可有效避免计算陷入局部收敛,从而得 到全局最优解[14]。基于此,作者通过单次压痕试验 与有限元模拟相结合的方法,结合反向分析方法与 模拟退火粒子群算法,从得到的载荷-深度曲线加载 部分提取材料的塑性参数,基于 Ludwig硬化模型 预测了不同金属材料的强度,并与单轴拉伸试验得 到的结果进行对比。

 1 试样制备与试验方法

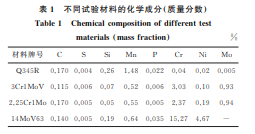
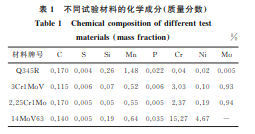
 试 验 材 料 包 括 Q345R 钢、3Cr1MoV 钢、 2.25Cr1Mo钢和 14MoV63 钢,均取自于服役后的 设备,化学成分如表1所示。在试验钢上截取尺寸 为30mm×30mm×15mm 的试样,采用 SPT-10 型仪器化压痕测试仪进行室温压痕试验,该设备位 移和载荷传感器精度分别为1μm 和0.1N,最大载 荷为5kN,下压速度设定为0.2mm·min -1,以确保 变形速率处于准静态应变范围。采用直径1.0mm 的碳化钨球形压头,压入深度为0.3mm,压痕比为 0.6。 表1 不同试验材料的化学成分 质量分数 Table1 Chemicalcompositionofdifferenttest materials massfraction % 材料牌号 C S Si Mn P Cr Ni Mo Q345R 0.170 0.004 0.26 1.48 0.022 0.04 0.02 0.005 3Cr1MoV 0.115 0.006 0.07 0.52 0.006 3.03 0.10 0.93 2.25Cr1Mo0.170 0.005 0.05 0.55 0.005 2.37 0.19 0.94 14MoV63 0.140 0.005 0.19 0.64 0.035 15.27 4.67 - 按照 GB/T228.1-2010,在试验钢上截取尺寸 为?6 mm ×30 mm 的 光 滑 圆 棒 拉 伸 试 样,在 Instron8800型拉伸试验机上进行室温拉伸试验, 拉伸速度为1mm·min -1。

 2 有限元模型的建立

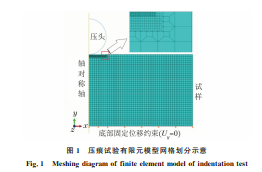
 采用 ABAQUS 软 件 进 行 压 痕 试 验 过 程 的 模 拟。由于压头与试样的结构具有轴对称性,因此为 节省计算时间,采用二维轴对称模型。在试样中只 取压头正下方略大于5倍压头半径的区域建模,此 时可忽略边界条件对模拟结果的影响[15]。压头视 为解析刚体,试样为变形体,其表面尺寸为4mm× 4mm,采用4节点轴对称缩减积分单元(CAX4R) 划分网格。约束试样底部y 方向的位移(Uy =0), 同时为压头施加固定位移约束。压头与试样之间建 立面-面接触,摩擦因数设为0.2,并用过渡网格细化 接触区域的网格。所建立的有限元模型如图1所示。

 3 强度计算方法 

3.1 本构方程的确定

 由于研究准静态条件下材料的强度时不需要考 虑材料的动态响应及损伤,故采用基本的弹塑性本 构方程。同时由于多数金属材料及合金的真应力与 86 黄礼洋,等:球压痕试验法评价金属材料的强度 图1 压痕试验有限元模型网格划分示意 Fig.1 Meshingdiagramoffiniteelementmodelofindentationtest 真应变关系可用幂指数进行拟合,因此采用 Ludwig 硬化模型[16],其表达式为 σ(εP)=σ0 +Kε n P (1) 式中:εP 为材料的真塑性应变;σ 和σ0 分别为材料 的真应力和初始屈服应力;K,n 分别为材料的强化 系数和应变强化指数。 

3.2 材料参数的识别 

通过对压痕试验曲线的反向分析得到材料的强 度。将由压痕试验得到的载荷-深度曲线视为材料 参数σ0,K,n 的函数,模拟曲线与试验曲线间的相 对误差[17]可表示为 F(σ0,K,n)= 1 N∑ N j=1 Fj,FE -Fj,Exp Fj,Exp (2) 式中:F 为模拟曲线与试验曲线的相对误差;N 为 ABAQUS软件中请求输出的数据点的个数;Fj,FE 和Fj,Exp 分别为某一压入深度下由模拟和试验得到 的载荷。 采用模拟退火粒子群算法从压痕载荷-深度曲 线中提取真应力-真塑性应变[18],其具体过程为:1) 预设一组材料参数σ0,K,n,并将其输入 ABAQUS 软件中模拟出对应的载荷-深度曲线;2)将模拟得到 的曲线与试验得到的曲线进行对比,用式(2)计算出 相应的误差函数;3)判断误差函数的大小,若其值小 于给定的值(此处设为0.5%)则计算终止,若该值大 于给定的值则根据模拟退火粒子群算法改变σ0,K, n,重新计算误差函数的大小,直到满足要求为止。

 3.3 强度的计算

 由于材料的强度是根据工程应力-应变曲线确 定的,因此所提取的真应力-真塑性应变曲线需先转 换为工程应力-应变曲线,转换公式为 εE =exp(εP +σ/E)-1 (3) σE = σ 1+εE (4) 式中:εE 为工程应变;σE 为工程应力;E 为弹性模 量。 将式(1)和式(3)代入式(4)中,得到工程应力与 真塑性应变的关系: σE = σ0 +Kε n P exp[εP + (σ0 +Kε n )/E] (5) 对于应力-应变曲线上无明显屈服平台的材料, 其屈服强度通常取工程塑性应变0.2%所对应的应 力。0.2%工程塑性应变对应的真塑性应变也约为 0.2%,将εP=0.002代入式(5)中即可计算出材料的 屈服强度。 材料的抗拉强度取拉伸试验中材料达到最大载 荷时所对应的工程应力,应用拉伸失稳的概念[19]得 到材料处于最大载荷处时满足: dσ dε =σ (6) 将式(6)变换为 dσ dε = dσ dεP × dεP dε (7) 由式(1)可以得到: dσ dεP =nKε n-1 P (8) 由于ε=εP+σ/E,结合式(7)和式(8),式(6)最 终可变换为 dσ dε =nKε n-1 P E E +nKε n-1 P =σ (9) 联立式(1)和式(9),即可得到εP 及其对应的抗 拉强度,其详细推导过程参考文献[18]。

 4 结果与讨论

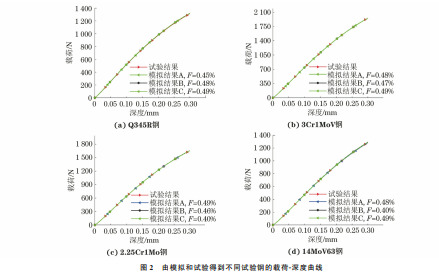
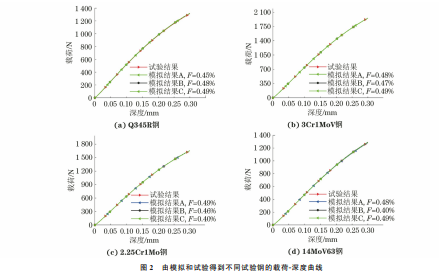
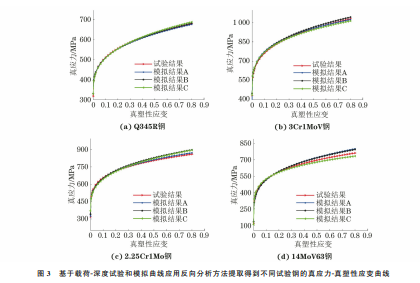
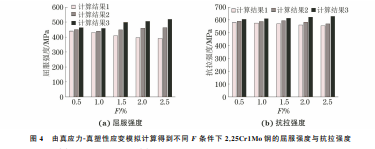
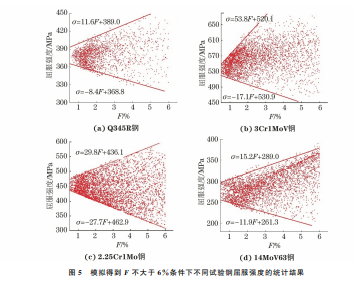
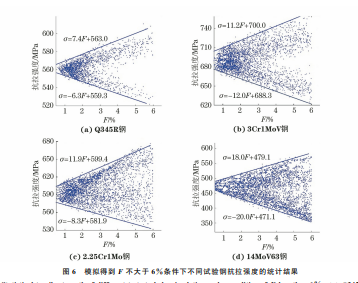
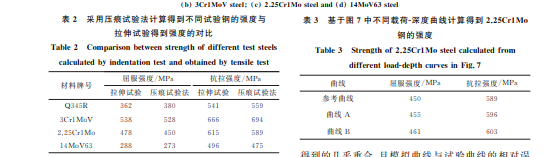
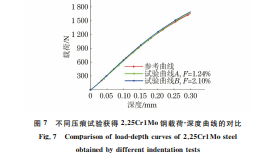
 由图2可以看出:由模拟得到的载荷-深度曲线 与试验得到的几乎重合,且模拟曲线与试验曲线的 相对误差F 均小于0.5%,说明模拟退火粒子群算 法能有效地从压痕载荷-深度曲线中提取出材料的 塑性参数。由图3可以看出:即使模拟得到的载荷深度曲线与试验得到的高度重合,但由反向分析方 法提取出的真应力-真塑性应变曲线仍不是唯一的, 这说明仅从单次压痕试验获得的载荷-深度曲线中 并不能提取出一组唯一的塑性参数,与前人的研究 结果一致[12,20]。这是由于模拟曲线是在假定材料 是均匀的、各向同性的条件下得到的,而实际材料并 未完全符合该假设,而且实际材料的硬化关系也不 能完全符合给定的硬化模型。 由于从载荷-深度曲线提取到的真应力-真塑性 87 黄礼洋,等:球压痕试验法评价金属材料的强度 图2 由模拟和试验得到不同试验钢的载荷-深度曲线 Fig 2 Load-depthcurvesofdifferentteststeelsobtainedbysimulationandtests a Q345Rsteel b 3Cr1MoVsteel c 2 25Cr1Mosteeland d 14MoV63steel 图3 基于载荷-深度试验和模拟曲线应用反向分析方法提取得到不同试验钢的真应力-真塑性应变曲线 Fig 3 Extractedtruestress-trueplasticstraincurvesofdifferentteststeelsbyinversemethodbasedontestedandsimulatedload-depthcurves a Q345Rsteel b 3Cr1MoVsteel c 2 25Cr1Mosteeland d 14MoV63steel 应变曲线不具有唯一性,因此从真应力-真塑性应变 曲线计 算 得 到 的 强 度 也 具 有 明 显 的 分 散 性。 以 2.25Cr1Mo钢 为 例,列 出 了 当 F 分 别 为 0.5%, 1.0%,1.5%,2.0%,2.5%时,由真应力-真塑性应变 模拟曲线计算得到的屈服强度和抗拉强度。由图4 可以看出:当F 为0.5%时,计算得到的2.25Cr1Mo 钢的屈服强度在440~462 MPa,抗拉强度在581~ 605MPa;当F 增大至2.5%时,其屈服强度在390~ 518MPa,抗拉强度在558~628 MPa。可以发现,随 着F 的增大,强度的分散性也增大。由此推论,当F 88 黄礼洋,等:球压痕试验法评价金属材料的强度 取0时可获得唯一的强度。 为更加清晰地反映强度与F 的关系,对F 不大 于6.0%条件下模拟得到不同试验钢的屈服强度和 抗拉强度进行统计。由图5与图6可知,随着F 的 减小,强度的分布范围减小,且趋近于某一个数值, 同时强度存在明显的上下边界线,即由真应力-真塑 性应变曲线计算得到的强度具有明显的收敛趋势。 这是由于随着 F 的减小,从载荷-深度曲线提取出 的真应力-真塑性应变曲线逐渐趋近于材料的真实 应力-应变曲线。 图4 由真应力-真塑性应变模拟计算得到不同F 条件下2.25Cr1Mo钢的屈服强度与抗拉强度 Fig 4 Yieldstrength a andtensilestrength b of2 25Cr1MosteelunderdifferentFconditionscalculatedfromsimulated truestress-truestraincurves 图5 模拟得到F 不大于6%条件下不同试验钢屈服强度的统计结果 Fig 5 StatisticalyieldstrengthofdifferentteststeelsbysimulationunderconditionofFlessthan6% a Q345Rsteel b 3Cr1MoVsteel c 2 25Cr1Mosteeland d 14MoV63steel 求解图5与图6中上下边界线的交点,即可得 到材料的强度。由表2可知,采用压痕试验法得到 不同试验钢的强度均接近真实强度,屈服强度的最 大相对误差为5.9%,抗拉强度的最大相对误差为 4.3%。这说明采用压痕试验法可以准确地评价金 属材料的强度。 由于多次试验得到的载荷-深度曲线并不能保 证高度重合,因此为研究试验误差对结果的影响,对 2.25Cr1Mo钢进行了2次压痕试验,得到的载荷-深 度曲线(A 和 B)如图7所示。将图2(c)中的载荷深度试验曲线作为参考曲线,通过式(2)计算得到曲 线 A 和曲线 B与参考曲线的相对误差为1.24%和 2.10%。由图7中各曲线得到的强度如表3所示。 由表3可以看出:压痕试验所得载荷-深度曲线与参 考曲线的相对误差越大,计算得到的强度偏离由参 考 曲线计算得到的强度的程度越大,且曲线的相对 89 黄礼洋,等:球压痕试验法评价金属材料的强度 图6 模拟得到F 不大于6%条件下不同试验钢抗拉强度的统计结果 Fig 6 StatisticaltensilestrengthofdifferentteststeelsbysimulationunderconditionofFlessthan6% a Q345Rsteel b 3Cr1MoVsteel c 2 25Cr1Mosteeland d 14MoV63steel 表2 采用压痕试验法计算得到不同试验钢的强度与 拉伸试验得到强度的对比 Table2 Comparisonbetweenstrengthofdifferentteststeels calculatedbyindentationtestandobtainedbytensiletest 材料牌号 屈服强度/MPa 抗拉强度/MPa 拉伸试验 压痕试验法 拉伸试验 压痕试验法 Q345R 362 380 541 559 3Cr1MoV 538 528 666 694 2.25Cr1Mo 478 450 615 589 14MoV63 288 273 496 475 图7 不同压痕试验获得2.25Cr1Mo钢载荷-深度曲线的对比 Fig.7 Comparisonofload-depthcurvesof2.25Cr1Mosteel obtainedbydifferentindentationtests 误差 在 2.10% 时,计 算 得 到 强 度 的 相 对 误 差 为 2.4%,满足工程实际要求。

 5 结 论

 (1)有 限元模拟得到的载荷-深度曲线与试验 表3 基于图7中不同载荷-深度曲线计算得到2.25Cr1Mo 钢的强度 Table3 Strengthof2.25Cr1Mosteelcalculatedfrom differentload-depthcurvesinFig.7 曲线 屈服强度/MPa 抗拉强度/MPa 参考曲线 450 589 曲线 A 455 596 曲线 B 461 603 得到的几乎重合,且模拟曲线与试验曲线的相对误 差均小于0.5%,说明模拟退火粒子群算法可有效 地从压痕试验载荷-深度曲线中提取出金属材料的 塑性参数。 (2)基于Ludwig硬化模型,利用反向分析方法 从压痕试验载荷-深度曲线中提取的真应力-真塑性 应变曲线不是唯一的,但从真应力-真塑性应变曲线 计算得到的强度具有明显的收敛趋势。 (3)采用压痕试验法得到不同金属材料的强度 均接近于由拉伸试验得到的强度,屈服强度与抗拉 强度的最大相对误差分别为5.9%,4.3%,说明采用 压痕试验法可以准确地评价金属材料的强度。 

来源：材料与测试网