分享：高应变速率下SiCp/Al复合材料的动态力学性能及其本构关系

邬小萍,吕琴丽,杨 宽,杨中元,纪 红(国合通用测试评价认证股份公司,北京101400)

摘 要:利用分离式 Hopkinson压杆试验装置对体积分数15%SiCp/Al复合材料进行动态压缩试验,研究了该复合材料在500~2000s-1 高应变速率下的动态力学性能及其显微组织演变;基于试验数据,通过包含与应变速率和塑性应变相关的绝热温升软化项的Johnson-Cook本构模型对应力-应变曲线进行预测,并将模型预测结果与试验结果进行对比。结果表明:复合材料的应变速率强化效应不明显,但是该材料具有显著的应变强化效应;随着应变速率的增加,复合材料的变形类型由均匀变形向局部化变形转变,增强相颗粒破裂严重,绝热剪切带在局部区域形成并扩展;采用包含绝热温升软化项Johnson-Cook本构模型计算得到的应力-应变曲线与试验结果间的相对误差小于17%。

关键词:SiCp/Al复合材料;Johnson-Cook本构模型;高应变速率;本构关系;动态压缩中图分类号:TB33 文献标志码:A 文章编号:1000-3738(2021)09-0083-05

0 引 言

碳化硅颗粒增强铝基(SiCp/Al)复合材料具有密度低、比强度和比刚度高、热导率大、热膨胀系数小及耐磨性能好等优点。低体积分数SiCp/Al复合材料作为重要的轻量化材料,已广泛用于生产飞机、汽车等发动机风扇出口导流叶片、起落架制动器缸体以及刹车片等。在应用过程中,SiCp/Al复合材料不可避免会受到冲击、碰撞等动载荷的作用,以高83邬小萍,等:高应变速率下SiCp/Al复合材料的动态力学性能及其本构关系应变速率发生变形。但是,目前有关SiCp/Al复合材料在动态载荷下力学特性的研究还很少。大量研究[1-4]表明,材料在动态载荷下的力学性能与准静态载荷下的差异巨大。动态载荷下的力学特性及动态本构方程是获得准确数值模拟的前提,因此有必要对SiCp/Al复合材料的动态力学特性及动态本构关系模型进行研究。目前,普遍采用 Hopkinson压杆系统进行动态力学性能测试,该系统具有结构简单、操作方便、测量方法精巧、加载波形易控制等优点,在金属材料方面的应用较成熟,而在复合材料中的应用还在不断摸索中[5]。OOSTERKAMP[6]通过单轴压缩试验和分离 Hopkinson压杆试验对不同厚度试样的本构关系进行了分析,发现高应变速率下的应变速率敏感度与试样尺寸参数有很大关系。SALAS等[7]根据试验结果,建立了力学性能参数与应变速率的关系 表 达 式,修 正 了 本 构 模 型 中 的 弹 性 模 量。WANG等[8]为了研究碳纤维增强树脂基复合材料单向层合板在高应变速率下的力学特性,采用一个线弹性单元与多个 Maxwell体并联的方式,建立了复合材料黏弹性动态本构模型,并通过不同应变速率下的动态压缩试验,确定了本构模型中的相关参数。胡锐等[9]利用 Hopkinson高速压杆冲击试验系统对SiCp/Al复合材料的压缩破坏响应进行了研究,发现该复合材料是一种应变速率敏感材料,随着SiC含量的增加,复合材料应变速率敏感性增大,其破坏模式以垂直于载荷方向的增强相颗粒的剪切开裂为主。孔令超等[10]利用伺服式疲劳试验机和杆杆型冲击拉伸试验机对 TiC颗粒增强钛基复合材料的静动态力学性能进行了研究,得到不同应变速率下复合材料的应力-应变曲线,并利用有限元软件对其静/动态力学性能进行数值模拟。作者采用分离式 Hopkinson压杆试验装置对体积分数 15%SiCp/Al复合材料进行动态压缩试验,研究了该复合材料在500~2000s-1 高应变速率下的动态力学性能及其显微组织演变;基于试验数据,通过引入绝热温升软化项对Johnson-Cook本构模型进行修正,并将模型预测结果与试验结果进行对比,从而为SiCp/Al复合材料的设计、模拟等提供理论依据。

1 试样制备与试验方法

试验材料为体积分数15%SiCp/Al(以下简称15%SiCp/Al)复合材料,由北京有色金属研究总院提供,其初始组织如图1所示,由颗粒状SiC及铝基体组成。在试验材料上截取尺寸为?5mm×5mm的动态压缩试样,采用分离式 Hopkinson压杆装置(SHPB)进行动态压缩试验,压杆材料为高强弹簧钢,压杆直径为14.5 mm,应变速率分别为500,1000,1500,2000s-1,每个应变速率下取3组有效数据的平均值。压缩试验结束后,将试样研磨、抛光,用 Keller试剂腐蚀后,采用ZEISSAxio光学显微镜观察显微组织。图1 15%SiCp/Al复合材料的原始组织Fig.1 Originalmicrostructureof15%SiCp/Alcomposite

2 试验结果与讨论

2.1 动态力学性能

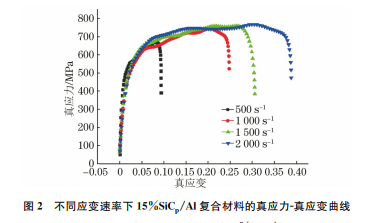
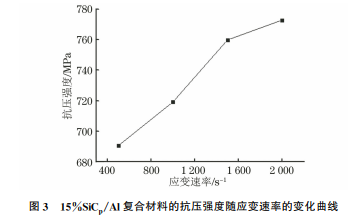
由图2可以看出:随着应变速率的增加,15%SiCp/Al复合材料的流变应力略有升高,但断裂应变明显增加,说明该复合材料具有明显的应变强化效应,而对应变速率不敏感;当材料进入塑性变形阶段后,随着应变的增大,流变应力出现较小的波动变化,这是由于随着应变的增大,高应变速率导致位错密度增加而产生加工硬化,在变形过程中,加工硬化与变形产生的热软化交替发生。图2 不同应变速率下15%SiCp/Al复合材料的真应力-真应变曲线Fig.2 Truestress-truestraincurvesof15%SiCp/Alcompositeatdifferentstrainrates由图3可以看出,复合材料的抗压强度随应变速84邬小萍,等:高应变速率下SiCp/Al复合材料的动态力学性能及其本构关系率增加而增大,并且当应变速率在500~1500s-1时,抗压强度的增加程度更显著,可见该材料在较低应变速率下的应变速率强化效应较突出。

2.2 显微组织变化

由图4可以看出:当应变速率为500s-1 时,复合材料 基 本 处 于 均 匀 变 形 状 态;当 应 变 速 率 为1000,1500s-1 时,复合材料中的增强相颗粒呈现规则有序排列,变形类型由均匀变形开始向局部化变形转变,这是因为15%SiCp/Al复合材料在高应变速率下压缩变形时,位错会切过尺寸较小的SiC颗粒或绕过尺寸较大的SiC颗粒,导致基体沿变形方向发生偏转而形成明显的塑性流变,同时压缩变形使SiC颗粒出现了不同程度的破裂,且随着应变速率的增加,破裂程度增加;当应变速率为2000s-1时,SiC颗粒破碎严重,基体中分布着大量破碎后的细小SiC颗粒。在压缩过程中,基体与增强相颗粒图4 不同应变速率下压缩后15%SiCp/Al复合材料的显微组织Fig.4 Microstructuresof15%SiCp/Alcompositeaftercompressionatdifferentstrainrates发生协同变形,应变速率的增加导致位错密度急剧增加,且没有足够的时间协调基体与SiC颗粒的变形,致使SiC颗粒在较大局部应力下破裂;同时大尺寸、多尖角的增强相颗粒由于局部应力较大且存在较多缺陷,在压缩过程中更易发生破裂。由图5可以看出:在应变速率为1500s-1 时,复合材料在动态压缩后出现了明显的变形不均匀区域,试样端面变形程度较小,内部中心区域变形程度较大,这可能与端面的摩擦效应有关;复合材料的变形局部化特征明显,组织中存在完整的绝热剪切裂纹,这是因为高应变速率变形引起低的应变硬化率和高的局部热量,这种非弹性功转化的局部热量将引起绝热温升,从而引起绝热剪切裂纹的形成和发展。图5 1500s-1 应变速率下压缩后15%SiCp/Al复合材料的组织Fig 5 Microstructureof15%SiCp Alcompositeaftercompressionatstrainrateof1500s-1 a particlefracturemorphology1 b particlefracturemorphology2 c microstructureofendfaceandinsideand d shearcrackingmorphology综上可知,在动态载荷条件下,15%SiCp/Al复合材料局部化变形及绝热剪切裂纹是逐步发展演化的过程。在应变速率较小时,复合材料处于均匀变形状态,随着应变速率的增加复合材料的变形特征向局部化变形转变,在高应变速率下局部化变形剧烈,绝热剪切带在局部区域形成并扩展。

3 本构模型的建立

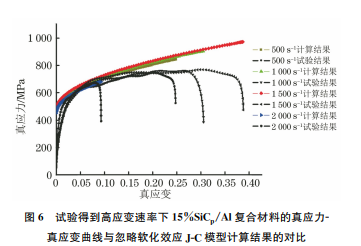
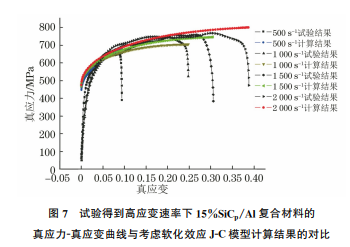
在工程材料研究中,常用的热-黏塑性本构模型有 Johnson-Cook 模 型 (J-C 模 型 )[11-12]、ZerilliArmstrong模型[13]、Power-Law模型[14]和Bammann模型[15]等。其中,J-C模型的形式较简洁,是一个与应变速率和温度相关的经验型理论模型,包含了材料的应变强化、应变速率强化和热软化参数,作者选85邬小萍,等:高应变速率下SiCp/Al复合材料的动态力学性能及其本构关系择J-C模型作为15%SiCp/Al复合材料的本构模型,该模型的表达式为σ=(A +Bεn )1+Clnε·ε· 0????????????????1-T -T0 TM -T0m ????????????????(1)式中:σ为应力;ε为等效塑性应变;ε·0 和ε· 分别为参考应变速率和等效塑性应变速率,ε·0 取0.002s-1;T,T0,TM 分别为环境温度、室温和材料的熔点;A,B,C,n,m 均为与材料有关的参数。(A+Bεn )、1+Clnε·ε· 0????????????????、1-T-T0 TM-T0m ????????????????分别描述了材料的应变强化效应、应变速率强化效应和热软化效应。静态常温条件(ε·=0.002s-1,T=296K)下,可忽略应变速率强化效应和热软化效应的影响,式(1)可变为σ=A +Bεn (2)式(2)两边取对数得到ln(σ-A)=lnB+nlnε (3)式中:A 为材料的屈服强度,取218MPa。对试验数据进行拟合,得到n为0.5041,B 为352.13。为了确定参数C,忽略热软化效应的影响,式(4)变为σA +Bεn =Clnε·ε· 0 +1 (4)取应变为0.25,应变速率分别为500,1000,1500,2000s-1 下的应力进行拟合,得到 C 为0.092。作者基于计算简便考虑,得到忽略热软化效应的15%SiCp/Al复合材料J-C模型为σ=(218+352.13ε0.5041)1+0.092lnε·ε· 0????????????????(5)图6为J-C模型计算结果与试验结果的对比,忽略热软化效应的J-C本构模型计算得到的应力应变曲线与试验结果间的相对误差为38%,由此可以看出,在高应变速率条件下,该本构模型不能很好地预测 SiCp/Al复合材料的流变应力,这是由于SiCp/Al基复合材料在高应变速率塑性变形过程中伴随着温度的升高,而温度的升高将引起材料的软化,因此J-C本构模型的建立应考虑软化作用。材料在动态变形过程中的绝热温升ΔT 可表示为ΔT =βρc∫pε0σdε (6)式中:ρ为材料的密度;cp 为材料的定压比热容;β为塑性功转化成热的因子。由于绝热温升是塑性应变的函数,为了简便起图6 试验得到高应变速率下15%SiCp/Al复合材料的真应力真应变曲线与忽略软化效应J-C模型计算结果的对比Fig.6 Comparisonfortestedtruestress-truestraincurvesof15%SiCp/AlcompositeathighstrainrateswithcalculatedresultsbyJ-Cmodelignoringsofteningeffect见,一些学者将J-C模型中的 1-T-T0 TM-T0m ????????????????转换为 一 项 与 应 变 速 率 和 塑 性 应 变 的 相 关 项1-ε·-1|ε· -1| kε????????????????(k为无量纲参数),用以考虑材料软化效应[16],因此本构模型变为σ=(A +Bεn )1+Clnε·ε· 0????????????????1-ε·-1ε· -1 kε????????????????(7)ε·-1|ε· -1| =10(ε·>500)(ε· ≤500)(8)考虑软化效应的J-C模型为一个与无量纲参数k相关的方程。对试验数据进行拟合,获得该无量纲参数k 为0.53。综上可知,考虑软化效应15%SiCp/Al复合材料的动态力学本构模型表示为σ=(218+352.13ε0.5041)·1+0.092lnε·ε· 0????????????????1-ε·-1ε· -1 0.53ε????????????????(9)由图7可知,与忽略软化影响的模型相比,考虑软化效应的本构模型计算得到的复合材料的真应力-真应变曲线与试验结果更加吻合,相对误差小于17%。

4 结 论

(1)15%SiCp/Al复合材料的流变应力均随应变速率的增大而略有升高,而断裂应变随着应变速率的升高而显著增大,说明该材料对应变速率不敏感,但具有明显的应变强化效应;当材料进入塑性变形阶段后,随着应变的增大,流变应力出现小幅波动;复合材料的抗压强度随应变速率增加而增大,且当应变速率在500~1500s-1 时,其增加程度更显著。86邬小萍,等:高应变速率下SiCp/Al复合材料的动态力学性能及其本构关系图7 试验得到高应变速率下15%SiCp/Al复合材料的真应力-真应变曲线与考虑软化效应J-C模型计算结果的对比Fig.7 Comparisonfortestedtruestress-truestraincurvesof15%SiCp/AlcompositeathighstrainrateswithcalculatedresultsbyJ-Cmodelconsideringsofteningeffect(2)随着应变速率的增加,复合材料的变形类型由均匀变形开始向局部化变形转变,增强相颗粒破裂严重,绝热剪切带在局部区域形成并扩展。(3)采用包含与应变速率和塑性应变相关的绝热温升软化项的J-C本构模型计算得到的复合材料的应力-应变曲线与试验结果间的相对误差小于17%,与忽略软化效应的模型相比,其预测结果与试验结果较吻合。

来源：材料与测试网