分享：退火过程中均质和异质结构纯铜晶粒的生长

孙书琪1,王润梓1,苑光健1,陈 浩1,高建宝2,彭 威1,张显程1,张利军2

(1.华东理工大学,承压系统与安全教育部重点实验室,上海 200237;2.中南大学,粉末冶金国家重点实验室,长沙 410083)

摘 要:通过相场模型和理想晶粒生长模型,模拟了均质结构及异质结构(梯度结构和双峰结构)纯铜在退火过程中的晶粒生长。结果表明:晶界能垒变化对均质结构晶粒生长速率的影响较小;退火时间大于600s时,均质结构晶粒的生长速率有一个较大的阶梯性变化;对于异质结构晶粒,晶界能垒越大,晶粒生长越慢;梯度结构中,小晶粒的生长速率最快,中晶粒的次之,大晶粒的最慢,且晶粒尺寸越大,晶界能垒对生长速率的影响越小;双峰结构中,晶界能垒对粗晶生长速率的影响较细晶的大,增加粗晶数目,细晶的生长速率明显降低,粗晶的生长速率增加。

关键词:相场模型;理想晶粒生长模型;均质结构;异质结构;晶界能垒中图分类号:TG111 文献标志码:A 文章编号:1000-3738(2021)06-0062-08

0 引 言

材料的性能由内部微观结构决定。对于大部分材料,析出强化、细晶强化、固溶强化等是常用的强化手段,但通常强度提高的同时韧性会降低[1-2]。随着加工方法与表征技术的发展,国内外学者在传统62孙书琪,等:退火过程中均质和异质结构纯铜晶粒的生长强化方法的基础上研究出一系列提高强度的同时又提高韧性的加工方法,如通过改变化学成分,使材料在变形过程中同时激活多种塑性变形机制,提高材料的韧性等。高熵合金通过元素短程强化,可以具有理想的力学性能[3]。对于纯铜及其他纯金属,通过形成异质结构,使材料内部产生大量应变不协调的组织,可以在提高强度的同时提高韧性[4-5]。异质结构微观上的主要特点是粗晶与细晶共存,粗、细晶共同作用影响材料的性能。在变形过程中,粗晶与细晶之间的尺寸差异导致材料无法自由的塑性变形,需要在粗晶晶界处产生位错来适应,从而产生协同强化作用。随着材料变形量增大,粗晶与细晶同时发生塑性变形,粗晶相对于细晶承受更大的塑性应变,在粗晶与细晶交界处产生应变梯度,使材料发生背应力加工硬化,从而提高材料韧性[6]。典型的异质结构为梯度结构和双峰结构,梯度结构是指晶粒尺寸从小到大呈梯度分布,双峰结构是指细晶中随机夹杂一个或数个粗晶的结构。CAI等[7]对 Cu-Zn合金表面进行机械研磨,得到梯度结构合金,通过室温拉伸试验发现合金具有较高的强度和韧性;FANG 等[8]制备的梯度纳米铜材料的表层硬度高达1.65GPa,耐磨性能改善。梯度结构材料表面强化层以及残余压应力场的存在,导致裂纹萌生位置从表面向次表面转移,从而提高了疲劳性能[9-10];SHAKOORI等[11]制备的双峰结构 Al6063合金超细晶区的屈服强度和抗拉强度高,粗晶区的延展性好;CAO 等[12]将细小的 WC 粉末加入粗晶粒 WC-Co硬质合金中,形成的双峰结构合金的硬度、耐磨性以及断裂韧性均得到较大提高。研究[13]表明,双峰结构对材料性能的改善程度低于梯度结构的。由于粗晶和细晶的热稳定性不同,由晶粒尺寸差异形成的异质结构会在退火过程中逐渐消失,导致材料服役性能明显降低。ZHANG 等[14]将含0.09%(质量分数)氮的梯度结构钽压块后进行退火,发现梯度结构消失,延展性下降;BACH 等[15]将双峰结构铜材进行398K×1h退火后,硬度下降约44%;HE等[16]发现双峰粒度分布对 Mg-8Gd-3Y0.5Zr合金强度的影响不大,合金强化主要归因于晶粒细化,且细晶生长会导致强度下降。异质结构中细晶多为纳米尺寸晶粒,为提高纳米晶的稳定性,MAYR等[17]在纯铜纳米晶中掺杂铋粒子至纳米晶晶界,降低了晶界能量,提高了晶界能垒(晶粒向周围晶粒生长扩散需要克服的能垒),有效抑制了纳米铜晶粒在退火过程中的晶粒生长,提高了纳米晶的稳定性。目前通过提高晶界能垒来抑制纳米晶粒生长的方法还未应用于异质结构,研究者们常采用模拟方法分析晶界能垒对异质结构晶粒生长的影响。相场法凭借其弥散界面的优势,通过耦合相场与溶质场、温度场以及其他外场,可模拟不同场作用下的晶粒生长过程,揭示异质结构的晶粒稳定机制。CHEN等[18]构建了单相晶粒长大的相场模型,并用该模型研究了单相、双相晶粒的粗化动力学和拓扑结构,发现模拟结果与理论接近;KAZARYAN 等[19]使用相场模型研究了各向异性的晶界迁移率对单晶生长形貌以及拓扑学的影响,发现晶界迁移率的各向异性对晶粒生长的影响非常小,而晶界能的各向异性对晶粒生长的影响较大;KRILL 等[20]通过改进算法克服了三维情况下需要计算过多相场变量的问题,将模型应用到三维晶粒的长大中;WU 等[21]使用相场晶体法研究了纳米晶的二维生长,发现不同取向差的纳米晶粒生长机制不同,取向差较小的晶粒在生长过程中发生了旋转;MIYOSHI等[22]使用相场法在超级计算机上对晶粒的生长进行了超大规模的模拟,实现了统计上具有足够数量的晶粒的真正稳态增长。为了研究晶界能垒对异质结构晶粒生长的影响,作者使用相场法对均质结构以及异质结构(梯度结构和双峰结构)纯铜晶粒的生长过程进行研究,重点分析了晶界能垒大小对不同结构纯铜在相同热处理条件下局部晶粒生长速率的影响,为纯铜材料的热处理提供参考。

1 模型与验证

1.1 相场模型

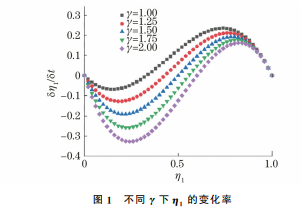
相场模型是描述材料微观结构演变的现象学手段,具有3个基本特征:(1)用连续场变量来描述材料的相态;(2)用连续场变量来表示系统能量;(3)用演化方程(通常为梯度流型方程)使驱动系统的自由能达到最小。相场模型中,多晶材料中的相是一个个具有独特取向的晶粒,晶粒长大的过程可通过相场的变化来表征。相场模型使用的相场变量数目与具有独特取向的晶粒数目相同,即具有p 个不同取向晶粒的系统需要p 个相场变量η1 (r,t),η2 (r,t),…,ηp(r,t)来描 述。相 场 变 量 是 时 间t 与 位 置r 的 函63孙书琪,等:退火过程中均质和异质结构纯铜晶粒的生长数,通过下标 将 每 个 相 场 变 量 映 射 到 晶 粒 的 取 向上。通过在某一点上晶粒i的相场变量η1=1,其余相场变量的值为0来描述该点上晶粒i的存在,而在晶界处,相场变量会在0~1之间连续变化,形成弥散界面。系统的总自由能是相场变量及其梯度项的函数,表达式为F =∫Vf(η1,…,ηp,η1,…,ηp)dV (1)将式中的相场变量项与其梯度项分开,表达式为F =∫Vf0(η1,η2,…,ηp)+k2∑pi=1???(ηi)2?????????????????????dV (2)式中:F 为系统的总自由能;k 为能量梯度系数(当模拟系统为各向同性时,k 为常数,各向异性时,k为变量);V 为体积;ηi 为相场变量;f0 为局部自由能密度。f0 的表达式[23]为f0(η1,η2,…,ηp)=∑pi=1β4η4i -α2η2 i +γ∑pi=1 ∑pj>iη2iη2j +14(3)式中:α 和β为能量常数;γ 为改变晶界能大小的现象学参数,不小于α/2。f0 在(η1,η2,…,ηp)=(±1,0,…,0),(0,±1,…,0),…,(0,0,…,±1)等2p 个点均取最小值0。由式(3)可以看出f0 的值与γ 相关。γ 主要影响局部自由能密度分布中能垒的位置,可通过变化γ 值来改变f0 的大小,从而改变晶界能的大小[24]。由于相场变量η是非保守变量,根据 GinzburgLandau方程假设其随时间的变化率与自由能对相场变量的变分成线性关系,则相场变量关于时间的变化率与自由能关系的表达式[18]为∂ηi∂t=-LδFδηi(4)式中:L 为与晶界迁移率相关的弛豫系数(模拟系统为各向同性时,L 为常数)。对式(2)和式(3)在晶界上积分得到晶界能的表达式为σij =∫+-????????????mf0(0,…,ηi,ηj,…,0)-fmin +κij2dηi dt2+κij2dηj dt2????????????dx (5)式中:σij 为晶界能;m 为模型参数[24];fmin 为自由能函数f0 的最小值;κij 为晶粒i,j 之间的能量梯度系数。将式(2)、式(3)和式(4)联立,得到∂ηi∂t=-Li -αηi +βη3i +γηi∑Pj≠iη2j -ki2 ηi(i=1,2,…,p) (6)使用显式 Euler迭代公式对式(6)的时间t进行离散化处理,表达式为ηi(t+Δt)=ηi(t)+dηi(t)dtΔt (7)式中:Δt为时间间隔。在空间上,使用五点差分法求解拉普拉斯算子(2η)i,j,表达式为(2η)i,j =ηi+1,j +ηi-1,j +ηi,j+1 +ηi,j-1 -4ηi,jh2(8)式中:h 为网格间距。对粒子掺杂至晶界的工艺进行模拟,研究晶界能垒对晶粒生长的影响。根据式(6)得到一维尺度上单相双晶分布中γ 对η1 变化率的影响,如图1所示,其中η1 处于0到1之间的部分即为晶界(晶内η1 的值为0或1)。由图1可以看出,γ 越大,η1 关于时间的变化率越小,说明晶界上相场变量的演化越困难,即晶界能垒越高。因此可采用不同γ 值来代表模拟过程中晶界能垒的不同。图1 不同γ 下η1 的变化率Fig.1 Changerateofη1 withdifferentγ

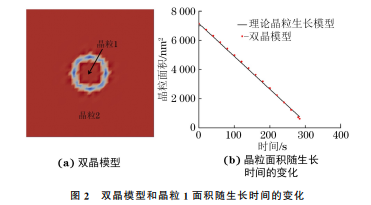
1.2 理想晶粒生长模型

理想晶粒生长模型[25]的表达式为Dn -Dn0 =kt (9)式中:D0 和 D 分别为生长前后的晶粒尺寸,nm;t为晶粒生长的时间,s;k 为与材料和晶粒生长温度相关的常数,nm·s-1;n 为晶粒生长指数,理想晶粒生长情况下,n 的值为2。为验证相 场 模 拟 晶 粒 生 长 的 合 理 性,设 计 如64孙书琪,等:退火过程中均质和异质结构纯铜晶粒的生长图2(a)所示的双晶模型,其中晶粒1生长完全由曲率驱动,符合理想晶粒生长条件。由图2(b)可以看出,双晶 模 型 中 晶 粒 1 生 长 时 的 晶 粒 面 积 与生长时间呈 线 性 关 系,与 理 论 晶 粒 生 长 模 型 曲 线吻合良好,并 且 与 他 人 对 单 晶 模 型 晶 粒 演 化 的 预测结果相符[25]。图2 双晶模型和晶粒1面积随生长时间的变化Fig.2 Bicrystalmodel(a)andchangeofareaofgrain1withgrowthtime2 研究方法在二维均质结构及异质结构纯铜合金晶粒长大过程中,晶界界面能和晶界迁移率均为各向同性。在纯铜中掺杂铋粒子时,粒子一般会作用在纯铜晶界上,可通过改变γ 值改变晶界能,从而抑制晶粒生长,且晶界上的铋粒子对纯铜非晶界部分的影响并 不 大[17]。 为 此,作 者 选 用 SCH?NFELDER等[26]在纯铜晶界迁移的分子动力学研究中得到的参数,通过改变γ 值来改变晶界能。ˇCí?EK 等[27]研究表明,纯铜晶粒发生异常长大的温度在433K 以上。因此模拟时的退火温度设为450K。在模拟过程中将系统离散为正方形网格,并采用周期性边界条件,取参数α=β=1,计算网格点总数为256×256,网格间距为0.125nm,计算过程中所有网格点处理1次计为1个时间步,最终模拟得到纯铜晶粒的长大过程。对于均质结构晶粒,采用 VoronoiTessellation(VT)法[28]建模,设置1.00,1.25,1.50,1.75,2.00等5组γ 值进行模拟,温度设置为450K。为了验证模拟结果的准确性,设计一组γ=1.50,退火温度为423K的纯铜退火试验,试验条件与 WANG 等[29]的研究相同,将模拟结果与试验结果进行对比。对于异质结构晶粒,采用更改模型形成条件的VT 法建立晶粒结构的初始物理模型,梯度结构的晶粒尺寸比为1∶5∶25,双峰结构细、粗晶粒尺寸比为1∶15,设置1.0,1.5,2.0 等 3 组γ 值进行模拟。针对双峰结构,在原模型中增加一个粗晶,探究不同初始双峰结构对晶粒生长速率的影响。由于异质结构中晶粒尺寸差距较大,晶粒生长曲线难以比较,故对晶粒面积做归一化处理(每个时间步的晶粒面积除以晶粒的初始面积)。

3 结果与分析

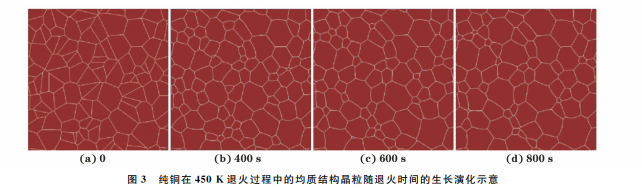
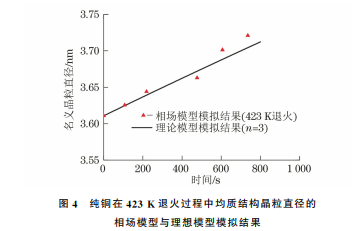
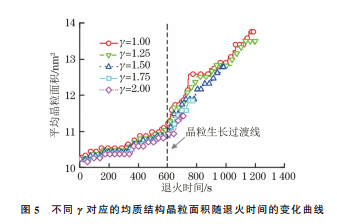
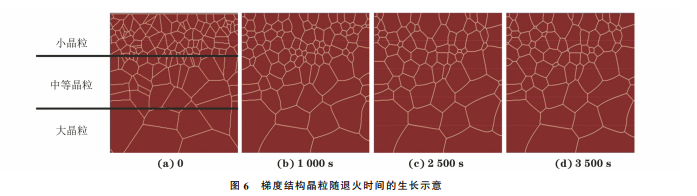
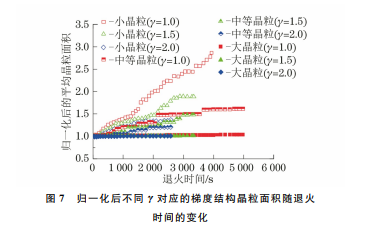
3.1 均质结构晶粒的长大由图3可以看出:在均质结构晶粒的长大过程中,大晶粒逐渐长大而小晶粒逐渐被吞噬直至消失;在晶粒长大初期,晶界曲率较小,随着晶粒长大,晶界曲率逐渐变大,三叉晶界夹角趋向120°。这是由于相场模拟晶粒长大过程中,晶粒演化的过程是系统从不稳定向稳定转变的演化过程,而三叉晶界夹角为120°是一个稳定的状态。此外,晶粒的整体平均尺寸增大。这种演化模式与罗志荣等[30]对均质结构晶粒生长的相场模拟结果基本一致。为了验证理想晶粒生长模型模拟均质结构晶粒生长的准确性,采用该模型模拟均质结构纯铜在温度423 K 下 退 火 时 的 晶 粒 生 长 行 为,取 γ 值 为1.50,根据 WANG 等[29]的试验结果,式(9)中k 取6.0×10-3 nm·s-1。由图4可以看出,当理想晶粒生长模型中的晶粒生长指数n=3时,纯铜退火过程中晶粒生长的相场模型模拟结果与理想模型的一图3 纯铜在450K 退火过程中的均质结构晶粒随退火时间的生长演化示意Fig.3 Diagramofgrowthandevolutionofuniformstructuralgrainswithannealingtimeofpurecopperduringannealingat450K65孙书琪,等:退火过程中均质和异质结构纯铜晶粒的生长致性较好(理想晶粒生 长 模 型 中 的n=2[31],但 实际由于织构、微观 结 构 存 在 异 质 性,n 值 处 于 2~8之间[31]),且 与 SIM?ES等[32]关 于 纯 铜 薄 膜 中纳米晶退火过程的晶粒生长指数为3时的模拟结果相符。图4 纯铜在423K 退火过程中均质结构晶粒直径的相场模型与理想模型模拟结果Fig.4 Phase field and ideal model simulation of uniformstructuralgraindiameterofpurecopperduringannealingat423K由图5可以看出,随着退火时间延长,晶粒面积图5 不同γ 对应的均质结构晶粒面积随退火时间的变化曲线Fig.5 Variationcurvesofuniformstructuralgrainareacorrespondingtodifferentγvsannealingtime增大,不同γ 下的晶粒面积相差不大;退火时间小于600s时,晶粒的生长速率较小,大于600s时生长速率有较明显的阶梯性变化,与 CAO 等[33]的研究结果相符。3.2 梯度结构晶粒的长大由图6可以看出,小晶粒的生长特征与均质结构晶粒的一致,大晶粒晶界曲率增大,但尺寸变化不明显。图6 梯度结构晶粒随退火时间的生长示意Fig.6 Diagramofgrowthofgradientstructuralgrainswithannealingtime图7 归一化后不同γ 对应的梯度结构晶粒面积随退火时间的变化Fig.7 Curvesofgradientstructuralgrainareacorrespondingtodifferentγvsannealingtimeafternormalizatim由图7可以看出:小晶粒的生长速率最快,中晶粒次之,大晶粒几乎不生长,对γ=1.5的晶粒生长曲线进行线性拟合,得到小晶粒、中晶粒和大晶粒的生长速率之比为76∶22∶1;γ 对小晶粒生长的影响最大,对中晶粒的影响次之,对大晶粒的影响最小;γ 越大,晶粒生长速率越慢,并且γ=1.0的中晶粒生长速率大于γ=2.0的小晶粒生长速率。大尺寸晶粒的生长速率慢,这是由于晶粒的生长是大晶粒吞噬周围小晶粒的过程,而大晶粒周围没有可供吞噬的小晶粒,并且大晶粒的稳定性高于小晶粒。通过线性拟合,得到当γ 从1.0增至2.0时,梯度结构小晶粒、中 晶 粒、大 晶 粒 的 生 长 速 率 分 别 降 低 了65%,31%,17%,说明晶粒尺寸越大,γ 对晶粒生长的影响越小。GUO等[34]研究表明,梯度结构铜在经过473K退火后,表 层 的 细 晶 平 均 尺 寸 从 0.65μm 增 长 到5.5μm,中心层晶粒从2.6μm 增加到4.3μm,从表层到中心层,晶粒生长速率减慢,且中心层的大晶粒生66孙书琪,等:退火过程中均质和异质结构纯铜晶粒的生长长非常缓慢。作者关于不同尺寸晶粒的生长趋势的模拟结果与 GUO等[34]的研究结果基本一致。

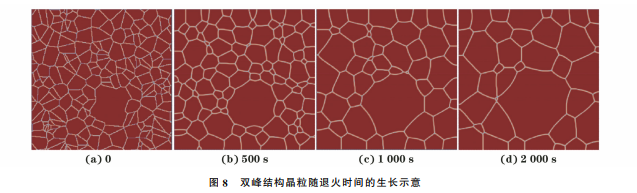
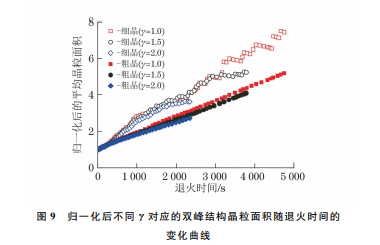
3.3 双峰结构晶粒的长大由图8可以看出,双峰结构中的大晶粒以及细晶的生长特征均与均质结构晶粒的相同,晶粒尺寸总体增大,三叉晶界的夹角趋于120°。由图9可以看出:双峰结构中的粗晶与细晶均有明显的生长,γ=1.5时,细晶的生长速率是粗晶的1.52倍;γ 对大晶 粒 和 细 晶 尺 寸 均 有 明 显 的 影响,随着γ 增大,晶粒生长速度降低,γ 从1.0增加到2.0时,细晶的生长速率降低了12%,粗晶降低了18%,说明γ 对粗晶的影响较大;与梯度结构晶粒的生长演化趋势相比,双峰结构中的粗晶生长较明显,这是由于梯度结构中大晶粒周围基本都是相对较大的晶粒,而双峰结构中大晶粒周围分布有小晶粒,晶粒生长的驱动力等于相邻晶粒尺寸的收缩量,具有低局部边界能的小晶粒容易被周围异常大的晶粒吞并[35],造成双峰结构中大晶粒的增长明显。图8 双峰结构晶粒随退火时间的生长示意Fig.8 Diagramofgrowthofbimodalstructuralgrainswithannealingtime图10 增加一个粗晶后,γ=1.5时双峰结构晶粒随退火时间的生长示意Fig.10 Diagramofgrowthofbimodalstructuralgrainswithannealingtimeatγ=1.5afteraddingacoarsegrain图9 归一化后不同γ 对应的双峰结构晶粒面积随退火时间的变化曲线Fig.9 Curvesofbimodalstructuralgrainareaafternormalizationcorrespondingtodifferentγvsannealimgtime纯铜在150 ℃以上退火时,大晶粒与小晶粒均发生 显 著 生 长,与 ZIELINSKI等[36]的 研 究 结 果相符。对γ=1.0的梯度结构和双峰结构晶粒尺寸的变化曲线进行对比,发现退火时间为4000s时,梯度结构小晶粒、中晶粒、大晶粒的面积分别是初始的2.7倍、1.55倍、1.05倍,而双峰结构中的粗晶面积为初始的4.3倍,细晶面积为初始的6.7倍左右,可见双峰结构的热稳定性较差。

3.4 初始双峰结构

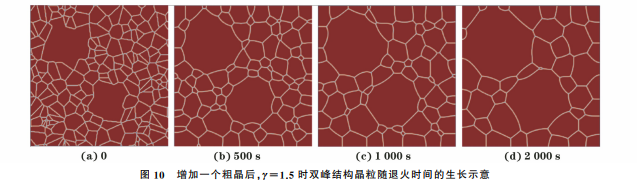
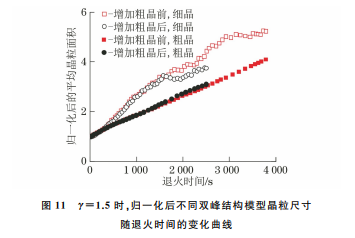
对晶粒长大的影响在双峰结构原始模型的粗晶对角位置上增加一个粗晶,模拟γ=1.5 的晶粒的生长过程,如图 10所示。由图11可以看出,增加一个粗晶后,随退火时间延长,细晶的生长速率明显降低,粗晶的生长速率增加了11%。粗晶生长靠吞噬周围的细晶进行,增加粗晶数目会使得该区域内的细晶生长受到抑制,生长速率降低,这与 WEIHNACHT 等[37]观察到的试验现象相符。

4 结 论

(1)晶界能垒变化对均质结构晶粒生长速率的影响较小,均质结构晶粒生长速率在退火时间大于600s时有一个较大的阶梯性变化。(2)对于异质结构,晶界能垒越大,晶粒生长越慢;梯度结构中,小晶粒的生长特征与均质结构晶粒的一致,大晶粒尺寸变化不明显;小晶粒的生长速率最快,中晶粒的次之,大晶粒的最慢;晶粒尺寸越大,晶界能垒对晶粒生长速率的影响越小。(3)双峰结构中,大晶粒与正常晶粒的生长特征均与均质结构晶粒的一致;晶界能垒对粗晶生长速率的影响较细晶的大;增加粗晶数目,细晶的生长速率明显降低,粗晶的生长速率增加。

来源：材料与测试网